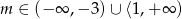Zadanie nr 9723778
Wyznacz wszystkie wartości  , dla których nierówność
, dla których nierówność 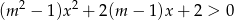 jest prawdziwa dla każdego
jest prawdziwa dla każdego 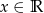 .
.
Rozwiązanie
Sprawdźmy najpierw co się dzieje gdy nierówność jest liniowa, czyli dla 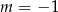 i
i 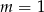 . Dla
. Dla 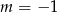 mamy nierówność
mamy nierówność 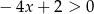 , a dla
, a dla 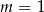 nierówność
nierówność 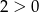 . Tylko druga z nich jest zawsze spełniona.
. Tylko druga z nich jest zawsze spełniona.
Jeżeli nierówność jest kwadartowa to jej wykres musi mieć ramiona skierowane do góry, czyli
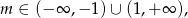
oraz musi być 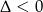 , czyli
, czyli
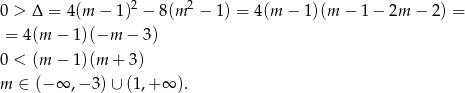
Łącząc otrzymane warunki otrzymujemy
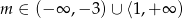
Odpowiedź: