Zadanie nr 6646612
Wykaż, że nie istnieją liczby  i
i 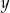 , takie, że
, takie, że 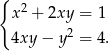
Rozwiązanie
Przekształcamy podany układ równań
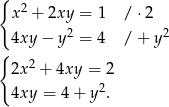
Podstawiamy drugie równanie do pierwszego i otrzymujemy
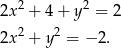
Zauważmy, że lewa strona tego równania jest zawsze większa bądź równa 0. Natomiast prawa strona jest stale ujemna jest to zatem równanie sprzeczne.

