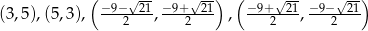/Szkoła średnia/Równania/Układy równań/Stopnia 2

Zadanie nr 8256230

Rozwiąż układ równań 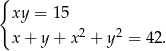{ xy = 15 x+ y+ x2 + y2 = 42.

Wersja PDF

Rozwiązanie

Sposób I

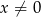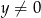Z pierwszego równania widać, że x ⁄= 0 i y ⁄= 0 , możemy więc wyliczyć z niego 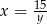x = 1y5 . Podstawmy to wyrażenie do drugiego równania.

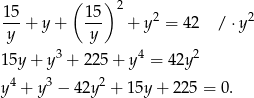
( )2 15- 15- 2 2 y + y + y + y = 4 2 / ⋅y 3 4 2 15y + y + 225 + y = 4 2y y4 + y3 − 42y2 + 15y + 225 = 0.

Aby rozwiązać otrzymane równwnie wielomianowe szukamy jego pierwiastków całkowitych wśród dzielników wyrazu wolnego. Po kilku sprawdzeniach można znaleźć pierwiastek 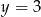y = 3 . Dzielimy wielomian przez 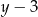y − 3 . My zrobimy to grupując wyrazy

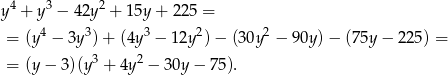
y 4 + y 3 − 42y 2 + 15y+ 225 = 4 3 3 2 2 = (y − 3y )+ (4y − 12y )− (30y − 90y )− (75y − 225) = = (y− 3)(y3 + 4y2 − 30y − 75).

Ponownie szukamy pierwiastków całkowitych i ponownie znajdujemy 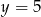y = 5 . Dzielimy dalej przez y− 5 .

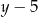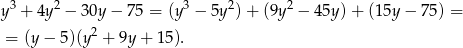
3 2 3 2 2 y + 4y − 3 0y− 75 = (y − 5y ) + (9y − 45y )+ (1 5y− 75) = = (y− 5)(y2 + 9y+ 15).

Rozwiązujemy otrzymane równanie kwadratowe 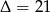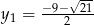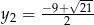Δ = 21 , − 9−√ 21- y1 = ---2--- , √-- y = −9+--21 2 2 . Otrzymujemy więc 4 pary rozwiązań (x ,y ) .

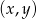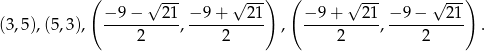
( √ --- √ --) ( √ --- √ --) − 9 − 21 − 9+ 21 − 9 + 21 − 9− 21 (3,5),(5,3), -----------,----------- , -----------,----------- . 2 2 2 2

Sposób II

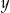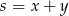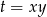Ponieważ oba równania są symetryczne względem x i y , możemy je zapisać w niewiadomych s = x + y i t = xy . Spróbujmy to zrobić

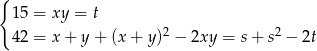
{ 15 = xy = t 42 = x + y+ (x+ y)2 − 2xy = s + s2 − 2t

Mamy zatem równanie

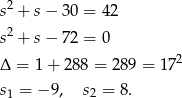
2 s + s− 30 = 42 s2 + s− 72 = 0 2 Δ = 1 + 288 = 289 = 17 s1 = − 9 , s2 = 8.

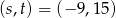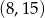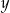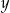Mamy zatem dwa rozwiązania (s,t) = (− 9,1 5) i (8,15) . Jak teraz obliczyć x i y ? Można rozwiązać odpowiedni układ równań, ale prościej jest skorzystać ze wzorów Viète’a. Liczby x i y są pierwiastkami równania

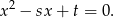
2 x − sx + t = 0.

Musimy zatem rozwiązać dwa równania

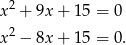
2 x + 9x + 1 5 = 0 x 2 − 8x + 1 5 = 0.

Pierwsze z nich rozwiązaliśmy już w sposobie I, a rozwiązaniem drugiego są liczby 3 i 5.  
Odpowiedź: ( √-- √ -) ( √-- √ -) (3,5),(5,3), −9−--21, −-9+-21 , −9+--21, −-9−-21 2 2 2 2

Wersja PDF