/Szkoła średnia/Równania/Układy równań/Stopnia 2

Zadanie nr 9562834

  • Wyznacz wszystkie liczby 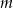m , dla których istnieją dwie liczby rzeczywiste, których suma i iloczyn są równe m .
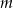  • Uzasadnij, że jeżeli suma i iloczyn dwóch liczb rzeczywistych jest równa liczbie dodatniej 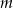m , to suma sześcianów tych liczb jest nie mniejsza niż 16.
Wersja PDF

Rozwiązanie

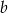  • Jeżeli a i b są liczbami o podanej własności, to mamy układ równań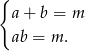
    { a + b = m ab = m .

    Podstawiając a z pierwszego równania do drugiego mamy

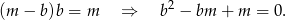
    (m − b)b = m ⇒ b2 − bm + m = 0.

    Równanie to ma rozwiązanie jeżeli 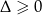Δ ≥ 0 . Zatem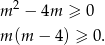

    2 m − 4m ≥ 0 m (m − 4) ≥ 0.

    Stąd m ∈ (− ∞ ,0⟩ ∪ ⟨4,∞ ) .  
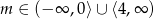    Odpowiedź: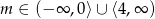 m ∈ (− ∞ ,0⟩∪ ⟨4,∞ )

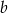  • Obliczmy sumę sześcianów liczb a i b takich, że 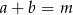a+ b = m i ab = m .
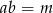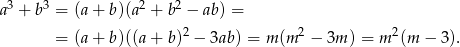
    a3 + b3 = (a + b)(a2 + b2 − ab) = 2 2 2 = (a + b)((a + b) − 3ab) = m (m − 3m ) = m (m − 3).

    Na mocy poprzedniego podpunktu wiemy, że 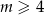m ≥ 4 zatem

    2 m (m − 3) ≥ 16 ⋅1 = 16.
Wersja PDF