Zadanie nr 5776977
Funkcja homograficzna 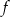 jest monotoniczna w przedziałach
jest monotoniczna w przedziałach 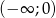 i
i 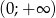 . Zbiór
. Zbiór 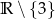 jest zbiorem wartości tej funkcji, a wartość 5 funkcja przyjmuje dla argumentu 3.
jest zbiorem wartości tej funkcji, a wartość 5 funkcja przyjmuje dla argumentu 3.
- Znajdź wzór funkcji
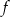 .
. - Wyznacz miejsce zerowe funkcji
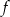 .
. - Wyznacz te argumenty, dla których funkcja
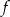 przyjmuje wartości większe od 1.
przyjmuje wartości większe od 1.
Rozwiązanie
- Najlepiej jest myśleć o wykresie funkcji (który jest hiperbolą), z podanych informacji wynika, że jego asymptoty to
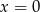 i
i 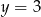 . Zatem ma ona wzór postaci
. Zatem ma ona wzór postaci 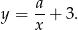
Współczynnik
 możemy wyznaczyć z warunku
możemy wyznaczyć z warunku 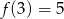 .
. 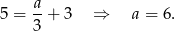
Odpowiedź: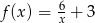
- Liczymy
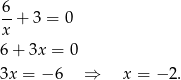
Odpowiedź: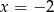
- Liczymy
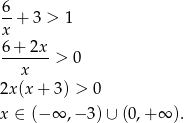
Na koniec, dla ciekawskich, wykres funkcji 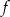 .
.
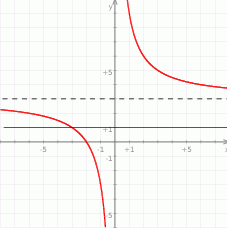
Odpowiedź: