Zadanie nr 8695539
Wyznacz wszystkie wartości parametru 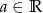 , dla których funkcja
, dla których funkcja 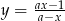 jest rosnąca w każdym przedziale, na którym jest określona. Dla
jest rosnąca w każdym przedziale, na którym jest określona. Dla 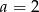 wyznacz zbiór wartości funkcji.
wyznacz zbiór wartości funkcji.
Rozwiązanie
Sposób I
Mamy do czynienia z funkcją homograficzną. Sprowadźmy ją do postaci kanonicznej.
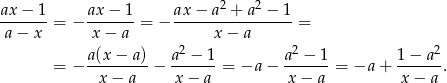
Widać teraz, że jest to hiperbola 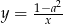 przesunięta o wektor
przesunięta o wektor ![[a,−a ]](https://img.zadania.info/zad/8695539/HzadR2x.gif) . Hiperbola ta jest rosnąca na przedziałach
. Hiperbola ta jest rosnąca na przedziałach 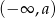 i
i 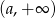 dokładnie wtedy, gdy licznik jest ujemny (dla
dokładnie wtedy, gdy licznik jest ujemny (dla 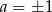 mamy stałą funkcję liniową). Mamy więc nierówność
mamy stałą funkcję liniową). Mamy więc nierówność
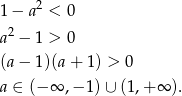
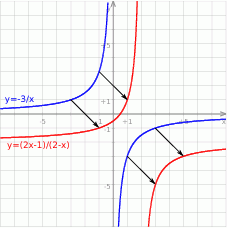
Dla 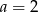 wykresem jest hiperbola
wykresem jest hiperbola 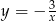 przesunięta o wektor
przesunięta o wektor ![[2,− 2]](https://img.zadania.info/zad/8695539/HzadR9x.gif) . Po naszkicowaniu tego wykresu widać, że zbiorem wartości jest zbiór
. Po naszkicowaniu tego wykresu widać, że zbiorem wartości jest zbiór 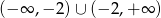 .
.
Sposób II
Dana funkcja będzie rosnąca na przedziałach określoności dokładnie wtedy, gdy jej pochodna będzie stale dodatnia. Liczymy pochodną.
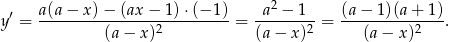
Widać teraz, że 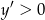 dla
dla 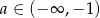 i
i 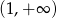 .
.
Dla 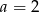 mamy funkcję.
mamy funkcję.
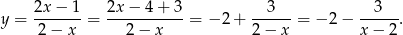
Jest to więc hiperbola 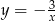 przesunięta o wektor
przesunięta o wektor ![[2,− 2]](https://img.zadania.info/zad/8695539/HzadR19x.gif) . Zbiorem wartości tej funkcji jest zbiór:
. Zbiorem wartości tej funkcji jest zbiór: 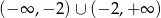 .
.
Sposób III
Sprawdzamy z definicji, kiedy funkcja 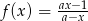 jest rosnąca na każdym z przedziałów
jest rosnąca na każdym z przedziałów 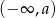 i
i 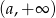 . Niech
. Niech 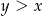 będą dwoma liczbami z jednego z tych przedziałów.
będą dwoma liczbami z jednego z tych przedziałów.
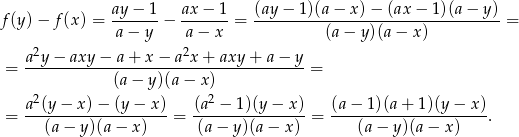
Ponieważ 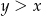 i liczby te są obie mniejsze lub większe od
i liczby te są obie mniejsze lub większe od  , powyższe wyrażenie jest dodatnie wtedy i tylko wtedy, gdy
, powyższe wyrażenie jest dodatnie wtedy i tylko wtedy, gdy 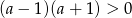 , czyli dla
, czyli dla 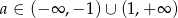 .
.
Dla 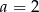 mamy funkcję.
mamy funkcję.
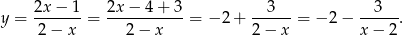
Jest to więc hiperbola 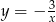 przesunięta o wektor
przesunięta o wektor ![[2,− 2]](https://img.zadania.info/zad/8695539/HzadR33x.gif) . Zbiorem wartości tej funkcji jest zbiór:
. Zbiorem wartości tej funkcji jest zbiór: 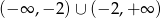 .
.
Odpowiedź: 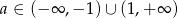 , zbiór wartości:
, zbiór wartości: 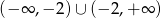 .
.

