/Szkoła średnia/Zadania maturalne/Matura 2009
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 4 kwietnia 2009 Czas pracy: 180 minut
W trójkącie prostokątnym 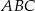 przyprostokątne mają długości:
przyprostokątne mają długości: 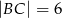 ,
, 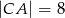 . Na boku
. Na boku 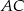 wybrano punkt
wybrano punkt 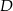 tak, że odcinki
tak, że odcinki 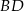 i
i 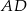 mają równe długości. Oblicz długość odcinka
mają równe długości. Oblicz długość odcinka 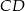 .
.
Dana jest funkcja 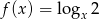 .
.
- Określ dziedzinę funkcji
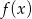 .
. - Naszkicuj wykres funkcji
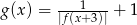 .
. - Odczytaj z wykresu maksymalne przedziały monotoniczności funkcji
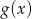 .
.
Wierzchołek 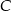 trójkąta
trójkąta 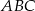 leży na okręgu o równaniu
leży na okręgu o równaniu 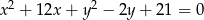 , a pozostałe wierzchołki mają współrzędne
, a pozostałe wierzchołki mają współrzędne 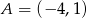 i
i 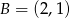 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia
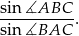
Opuszczone z wysokości 705,6 m ciało w ciągu pierwszej sekundy przebyło drogę 4,9 m, a w każdej następnej sekundzie przebyło drogę o 9,8 m dłuższą niż w poprzedniej sekundzie. Po ilu sekundach ciało spadło na powierzchnię Ziemi?
Oblicz prawdopodobieństwo, że w rzucie pięcioma sześciennymi kostkami do gry otrzymamy sumę oczek różną od 28.
Na bokach 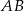 i
i 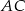 trójkąta
trójkąta 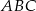 , który nie jest równoramienny, wybrano takie punkty
, który nie jest równoramienny, wybrano takie punkty 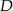 i
i 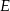 , że
, że 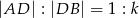 oraz
oraz 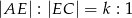 , dla
, dla 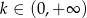 .
.
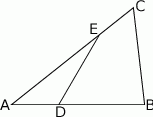
- Wyznacz wzór funkcji
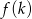 , która jest zdefiniowana jako stosunek pól trójkątów
, która jest zdefiniowana jako stosunek pól trójkątów 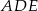 i
i 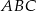 .
. - Wiedząc że
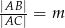 , dla
, dla 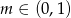 wyznacz wszystkie wartości parametru
wyznacz wszystkie wartości parametru 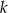 , dla których trójkąty
, dla których trójkąty 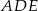 i
i 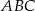 są podobne.
są podobne.
Wykres funkcji kwadratowej 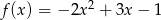 przesunięto o
przesunięto o 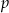 jednostek wzdłuż osi
jednostek wzdłuż osi 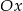 i o
i o 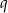 jednostek wzdłuż osi
jednostek wzdłuż osi 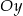 . Otrzymano w ten sposób wykres funkcji
. Otrzymano w ten sposób wykres funkcji 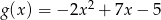 .
.
- Wyznacz liczby
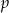 i
i 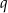 .
. - Rozwiąż równanie
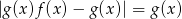 .
.
Rozwiąż nierówność 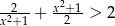 .
.
Ciąg 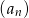 określony jest przez warunki
określony jest przez warunki 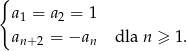
- Wypisz 6 początkowych wyrazów ciągu
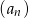 .
. - Oblicz sumę 20 początkowych wyrazów ciągu
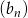 danego wzorem
danego wzorem 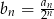 .
.
Dany jest wielomian 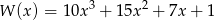 .
.
- Zapisz wielomian
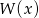 jako iloczyn wielomianów liniowych.
jako iloczyn wielomianów liniowych. - Określ dziedzinę funkcji
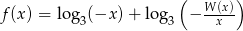 .
.
W stożek o promieniu podstawy 6 i wysokości 8 wpisujemy graniastosłupy prawidłowe sześciokątne tak, że jedna podstawa jest zawarta w podstawie stożka, a pozostałe wierzchołki należą do powierzchni bocznej stożka. Oblicz objętość graniastosłupa o największym polu powierzchni bocznej.

