/Szkoła średnia/Zadania maturalne/Matura 2009
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 2 maja 2009 Czas pracy: 180 minut
Rozwiąż nierówność 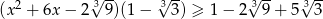 .
.
Punkt  jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 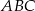 . Wierzchołek
. Wierzchołek 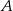 ma współrzędne
ma współrzędne 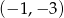 , a bok
, a bok 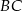 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 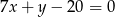 . Oblicz pole trójkąta
. Oblicz pole trójkąta 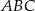 .
.
- Zaznacz w układzie współrzędnych zbiór
 punktów, których współrzędne
punktów, których współrzędne 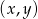 spełniają warunek:
spełniają warunek: 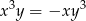 .
. - Wiedząc, że wykres funkcji homograficznej
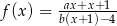 nie ma punktów wspólnych ze zbiorem
nie ma punktów wspólnych ze zbiorem 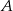 wyznacz
wyznacz  i
i 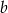 .
.
Pan Alojzy postanowił co miesiąc odkładać pewną sumę pieniędzy. W pierwszym miesiącu odłożył 100 zł, a w każdym następnym odkładał o 5% więcej niż w poprzednim. Razem z panem Alojzym oszczędzanie rozpoczęła jego małżonka, przy czym odłożyła ona w pierwszym miesiącu 110 zł, a w każdym następnym odkładała o 3% więcej, niż w poprzednim. Oblicz, która z tych dwóch osób zaoszczędzi więcej pieniędzy po roku oszczędzania.
Trapez równoramienny o podstawach długości 14 cm i 26 cm oraz o wysokości 6 cm obraca się wokół swojej osi symetrii. Oblicz objętość otrzymanej bryły.
Uzasadnij, że
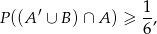
jeżeli 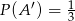 i
i 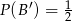 .
.
- Uzasadnij, że
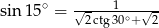
- W równoległoboku
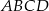 dane są miary kątów
dane są miary kątów 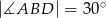 i
i 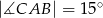 . Oblicz miarę kąta
. Oblicz miarę kąta 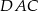 .
.
Ciąg 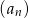 jest ciągiem arytmetycznym, w którym
jest ciągiem arytmetycznym, w którym 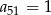 oraz wyrażanie
oraz wyrażanie 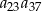 ma najmniejszą możliwą wartość. Wyznacz
ma najmniejszą możliwą wartość. Wyznacz 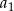 .
.
Liczby 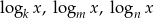 są kolejnymi wyrazami ciągu arytmetycznego, gdzie
są kolejnymi wyrazami ciągu arytmetycznego, gdzie 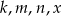 są różnymi od jedności liczbami dodatnimi. Uzasadnij, że
są różnymi od jedności liczbami dodatnimi. Uzasadnij, że 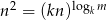 .
.
Wyznacz wszystkie wartości parametru 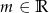 , dla których zbiór rozwiązań nierówności
, dla których zbiór rozwiązań nierówności
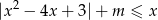
jest jednoelementowy.
Wielomiany 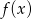 i
i 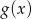 spełniają warunki
spełniają warunki 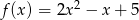 i
i 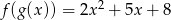 . Wyznacz wzór wielomianu
. Wyznacz wzór wielomianu 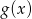 .
.

