/Szkoła średnia/Zadania maturalne/Matura 2009

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez portal www.zadania.info poziom podstawowy 14 marca 2009 Czas pracy: 120 minut

Zadanie 1
(3 pkt)

Wyrażenie 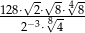√- √- 4√- 128⋅−23⋅8√8⋅-8 2 ⋅ 4 zapisz w postaci 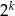2k , gdzie 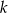k jest liczbą wymierną.

Zadanie 2
(5 pkt)

Rysunek przedstawia fragment wykresu funkcji określonej wzorem 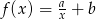f(x) = a + b x dla x ⁄= 0 .

PIC

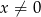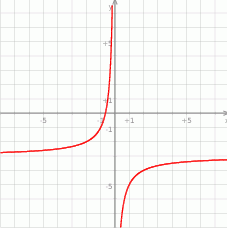
  • Odczytaj z wykresu rozwiązanie nierówności f(x) ≤ − 1 .
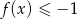  • Oblicz współczynniki a i b .

Zadanie 3
(4 pkt)

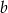Oblicz pole trójkąta ograniczonego prostą 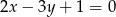2x − 3y + 1 = 0 i osiami układu współrzędnych.

Zadanie 4
(4 pkt)

Wiedząc, że liczba 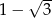√ -- 1 − 3 jest pierwiastkiem wielomianu 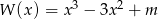3 2 W (x) = x − 3x + m , wyznacz wartość parametru m .

Zadanie 5
(4 pkt)

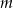Uczniowie pewnej szkoły zostali zabrani na wycieczkę do muzeum. W wycieczce wzięło udział 11 uczniów klasy pierwszej, 30 uczniów klasy drugiej i 9 uczniów klasy trzeciej. Przed wejściem do muzeum uczniowie zostali ustawieni w kolejce jeden za drugim. Oblicz prawdopodobieństwo tego, że pierwsi trzej uczniowie w tej kolejce to uczniowie drugiej klasy.

Zadanie 6
(5 pkt)

Romb o kącie ostrym 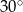30 ∘ jest opisany na okręgu o promieniu 2. Oblicz pole tego rombu.

Zadanie 7
(4 pkt)

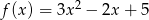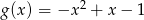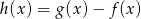Dane są dwie funkcje kwadratowe f(x) = 3x 2 − 2x + 5 i g(x) = −x 2 + x − 1 . Wyznacz największą wartość funkcji h(x) = g(x )− f(x) .

Zadanie 8
(3 pkt)

Długości obu podstaw trapezu wydłużono o 25%. O ile procent należy skrócić jego wysokość aby pole trapezu nie uległo zmianie?

Zadanie 9
(4 pkt)

Na narysowanej poniżej siatce sześcianu zaznaczono trzy środki ścian sześcianu.

PIC

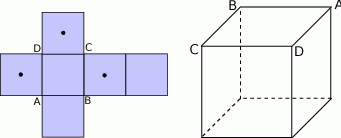
  • Zaznacz na powierzchni sześcianu trzy punkty 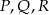P,Q ,R odpowiadające środkom ścian wskazanym na jego siatce.
  • Wiedząc, że krawędź sześcianu ma długość 1, oblicz pole trójkąta PQR .

Zadanie 10
(5 pkt)

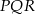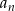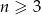Niech an , dla n ≥ 3 będzie liczbą krawędzi graniastosłupa prostego o podstawie będącej n -kątem foremnym.

  • Wyznacz wzór ciągu (an ) .
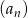  • Sprawdź czy ciąg 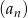(a ) n jest ciągiem arytmetycznym.
  • Uzasadnij, że żaden wyraz tego ciągu nie jest równy 2009.

Zadanie 11
(4 pkt)

W 10-wyrazowym ciągu arytmetycznym suma wyrazów o numerach nieparzystych jest równa 35. Oblicz piąty wyraz tego ciągu.

Zadanie 12
(5 pkt)

W pewnej szkole przeprowadzono ten sam sprawdzian z matematyki w trzech klasach 1a, 1b i 1c. Na poniższym diagramie przedstawiono wyniki tego sprawdzianu z wyszczególnieniem liczby osób, które uzyskały poszczególne oceny.

PIC

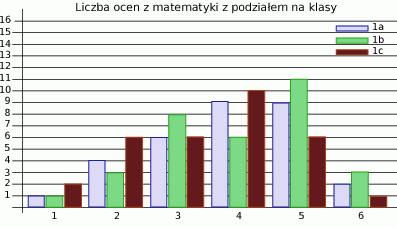
  • Ilu uczniów pisało sprawdzian w poszczególnych klasach?
  • Która z ocen była wystawiana najczęściej?
  • W której klasie średnia ocen ze sprawdzianu była najwyższa?

Arkusz Wersja PDF
Rozwiązania