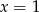/Szkoła średnia/Równania/Potęgowe i pierwiastki

Zadanie nr 2051250

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 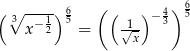( ∘ ----)6 (( ) 4) 6 3 − 12 5 √1- − 3 5 x = x .

Rozwiązanie

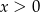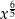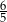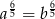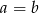Po pierwsze, aby napisane wyrażenia miały sens musi być x > 0 . Funkcja potęgowa 6 x5 jest różnowartościowa, więc od razu możemy sobie odpuścić wykładniki 6 5 po obu stronach (innymi słowy jeżeli 65 65 a = b to a = b ). Mamy zatem

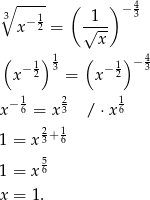
∘ ---- ( ) − 4 3 − 12 -1-- 3 x = √ x ( ) 1 ( ) 4 x −12 3 = x −12 −3 −16 23 16 x = x / ⋅x 1 = x23+ 16 5 1 = x6 x = 1.

Ostatnie przejście ponownie wynika z różnowartościowości funkcji 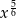5 x 6 , ponieważ dla 1 przyjmuje ona wartość 1, to jest to jedny punkt o tej własności.  
Odpowiedź: x = 1

Wersja PDF