/Szkoła średnia/Równania/Potęgowe i pierwiastki

Zadanie nr 5219902

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 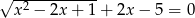√ -2---------- x − 2x + 1 + 2x − 5 = 0 .

Rozwiązanie

Przekształćmy podane równanie

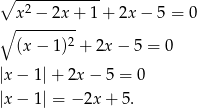
∘ -2---------- ∘ x-−--2x-+ 1 + 2x − 5 = 0 2 (x− 1) + 2x− 5 = 0 |x − 1|+ 2x − 5 = 0 |x − 1| = − 2x + 5.

Sposób I

Korzystając z definicji wartości bezwzględnej, otrzymane równanie możemy zamienić na dwa równania

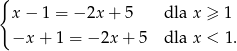
{ x− 1 = − 2x + 5 dla x ≥ 1 −x + 1 = − 2x + 5 dla x < 1.

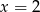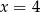Rozwiązania tych równań to odpowiednio x = 2 oraz x = 4 , jednak tylko pierwsze z nich spełnia odpowiadającą nierówność.

Sposób II

Tak jak poprzednio zauważamy, że wystarczy rozwiązać równanie

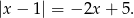
|x − 1 | = − 2x + 5.

Aby to równanie miało sens, prawa strona musi być nieujemna, czyli 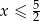x ≤ 5 2 . Przy tym założeniu, podane równanie jest równoważne dwóm równaniom (to dodatkowe założenie jest niezbędne, żeby wyeliminować sytuację typu 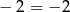− 2 = − 2 , która nie daje rozwiązania, bo |− 2| ⁄= − 2 )

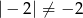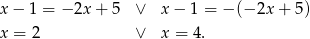
x− 1 = − 2x + 5 ∨ x− 1 = − (− 2x + 5) x = 2 ∨ x = 4.

Tylko pierwsze z tych rozwiązań spełnia nierówność 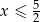x ≤ 5 2 .  
Odpowiedź: x = 2

Wersja PDF