/Szkoła średnia/Równania/Potęgowe i pierwiastki

Zadanie nr 5326580

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 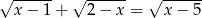√ ------ √ ------ √ ------ x − 1+ 2− x = x − 5 .

Rozwiązanie

Sposób I

Powinniśmy najpierw przyjrzeć się dziedzinie, ale zamiast tego na koniec sprawdzimy otrzymane rozwiązania. Przekształćmy podane równanie.

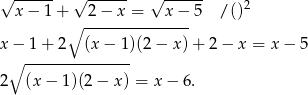
√ ------ √ ------ √ ------ 2 x − 1 + 2 − x = x − 5 /() ∘ --------------- x − 1 + 2 (x − 1 )(2 − x )+ 2 − x = x − 5 ∘ --------------- 2 (x − 1 )(2 − x ) = x − 6.

Zamiast liczyć to dalej zauważmy, że aby ta równość mogła być spełniona musi być 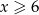x ≥ 6 (prawa strona musi być nieujemna). Wtedy jednak wyrażenie pod pierwiastkiem jest ujemne (bo pierwszy nawias jest dodatni, a drugi ujemny). Zatem równanie jest sprzeczne.

Sposób II

Zauważmy, że wyrażenie pod ostatnim pierwiastkiem jest nieujemne dla 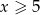x ≥ 5 , a wyrażenie pod drugim pierwiastkiem dla 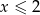x ≤ 2 . Ponieważ warunki te są rozłączne, równanie jest sprzeczne.

Wersja PDF