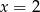/Szkoła średnia/Równania/Potęgowe i pierwiastki

Zadanie nr 6004825

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 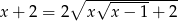∘ -√----------- x+ 2 = 2 x x − 1 + 2 .

Rozwiązanie

Powinniśmy najpierw przyjrzeć się dziedzinie, ale zamiast tego na koniec sprawdzimy otrzymane rozwiązania. Podnieśmy równanie stronami do kwadratu – taka operacja może dołożyć nam pewne fałszywe rozwiązania, ale tak czy inaczej mamy je posprawdzać.

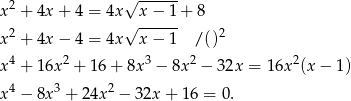
√ ------ x2 + 4x + 4 = 4x x − 1 + 8 2 √ ------ 2 x + 4x − 4 = 4x x − 1 / () 4 2 3 2 2 x + 16x + 16 + 8x − 8x − 32x = 16x (x − 1) x4 − 8x3 + 24x 2 − 3 2x+ 16 = 0.

Musimy rozwiązać to równanie wielomianowe. Szukamy najpierw pierwiastków całkowitych – łatwo znaleźć 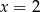x = 2 . Dzielimy wielomian przez 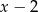x − 2 , my zrobimy to grupując wyrazy.

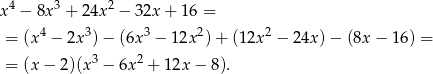
4 3 2 x − 8x + 2 4x − 32x + 16 = = (x 4 − 2x 3)− (6x3 − 12x2) + (12x 2 − 24x )− (8x− 16) = 3 2 = (x − 2)(x − 6x + 12x − 8).

Otrzymany wielomian stopnia 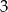3 nadal zeruje się dla 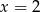x = 2 , więc dzielimy dalej przez x − 2 .

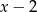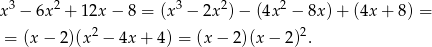
3 2 3 2 2 x − 6x + 12x − 8 = (x − 2x )− (4x − 8x )+ (4x + 8) = = (x− 2)(x2 − 4x + 4) = (x − 2)(x − 2 )2.

Zatem jedyny pierwiastek jaki otrzymaliśmy to 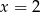x = 2 . Łatwo sprawdzić, że istotnie jest to pierwiastek wyjściowego równania.  
Odpowiedź: x = 2

Wersja PDF