/Szkoła średnia/Równania/Potęgowe i pierwiastki

Zadanie nr 7260505

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 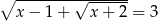∘ --------√------- x − 1 + x + 2 = 3 .

Rozwiązanie

Sposób I

Podnosimy równanie stronami do kwadratu (obie strony są nieujemne).

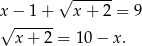
√ ------ x√ −-1-+- x + 2 = 9 x + 2 = 10− x.

Prawa strona musi być nieujemna, czyli 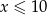x ≤ 10 . Przy tym założeniu możemy znowu podnieść równanie do kwadratu.

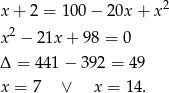
x + 2 = 100 − 20x + x 2 x 2 − 2 1x+ 98 = 0 Δ = 441 − 3 92 = 49 x = 7 ∨ x = 14.

Ze względu na nasze założenie rozwiązaniem jest tylko 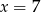x = 7 .

Sposób II

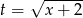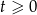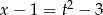Tym razem podstawmy √ ------ t = x + 2 . Wtedy t ≥ 0 oraz x − 1 = t2 − 3 . Mamy zatem równanie

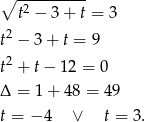
∘ -2-------- t − 3 + t = 3 t2 − 3+ t = 9 t2 + t− 12 = 0 Δ = 1+ 48 = 49 t = − 4 ∨ t = 3.

Ujemne rozwiązanie odrzucamy i mamy

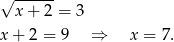
√ ------ x + 2 = 3 x + 2 = 9 ⇒ x = 7.

 
Odpowiedź: x = 7

Wersja PDF