/Szkoła średnia/Równania/Potęgowe i pierwiastki

Zadanie nr 9417869

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 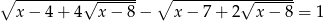∘ ---------√------- ∘ ---------√------- x − 4 + 4 x − 8 − x− 7+ 2 x − 8 = 1 .

Rozwiązanie

Sposób I

Zanim zajmiemy się dziedziną równania, spróbujmy je przekształcić.

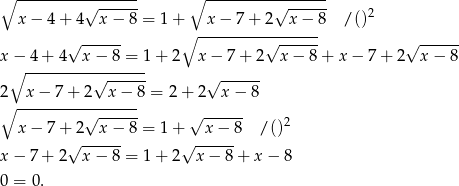
∘ ---------√------- ∘ ---------√------- x − 4 + 4 x − 8 = 1+ x − 7 + 2 x − 8 /()2 √ ------ ∘ ---------√------- √ ------ x− 4+ 4 x − 8 = 1 + 2 x− 7+ 2 x − 8 + x − 7 + 2 x − 8 ∘ ---------√------- √ ------ 2 x − 7 + 2 x − 8 = 2+ 2 x − 8 ∘ ----------------- x − 7 + 2√x--−-8-= 1+ √x-−--8- / ()2 √ ------ √ ------ x− 7+ 2 x − 8 = 1 + 2 x − 8 + x − 8 0 = 0.

Tak więc równanie jest zawsze spełnione, o ile ma sens, i o ile powyższe przejścia były równoważnościami (a tak jest, bo jeżeli podnosiliśmy równanie do kwadratu, to strony były nieujemne). Sprawdźmy jaka jest dziedzina równania.

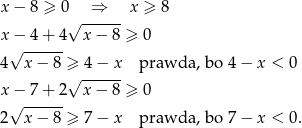
x − 8 ≥ 0√ -⇒----x ≥ 8 x − 4 + 4 x− 8 ≥ 0 √ ------ 4 x− 8 ≥ 4− x prawda, bo 4 − x < 0 √ ------ x −√ 7-+-2- x− 8 ≥ 0 2 x− 8 ≥ 7− x prawda, bo 7 − x < 0.

Zatem dziedziną równania jest zbiór 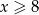x ≥ 8 .

Sposób II

Jeżeli dokładnie popatrzymy na poprzednie rozwiązanie, to można zauważyć, że

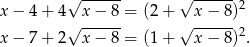
√ ------ √ ------ x − 4+ 4 x − 8 = (2 + x − 8 )2 √ ------ √ ------ x − 7+ 2 x − 8 = (1 + x − 8 )2.

Podane równanie możemy więc zapisać w postaci

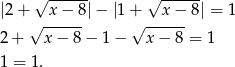
√ ------ √ ------ |2+ x − 8|− |1 + x − 8| = 1 √ ------ √ ------ 2+ x− 8− 1− x− 8 = 1 1 = 1.

Zatem równanie jest zawsze spełnione, o ile 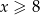x ≥ 8 .  
Odpowiedź: x ∈ ⟨8,+ ∞ )

Wersja PDF