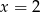/Szkoła średnia/Równania/Potęgowe i pierwiastki

Zadanie nr 9554995

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 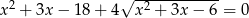2 √ -2---------- x + 3x − 18 + 4 x + 3x − 6 = 0 .

Rozwiązanie

Powinniśmy sprawdzić kiedy wyrażenie pod pierwiastkiem jest nieujemne, ale zamiast tego na końcu sprawdzimy otrzymane rozwiązania. Jeżeli podstawimy 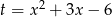t = x 2 + 3x − 6 to równanie ma postać

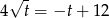
√ - 4 t = −t + 12

Widać, że musi być 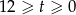12 ≥ t ≥ 0 . Przy tym założeniu możemy podnieść równanie stronami do kwadratu.

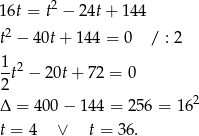
16t = t2 − 24t + 144 2 t − 40t+ 144 = 0 / : 2 1 2 --t − 2 0t+ 72 = 0 2 2 Δ = 400 − 14 4 = 256 = 1 6 t = 4 ∨ t = 3 6.

Ze względu na założenie musi być 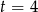t = 4 . Daje to nam równanie

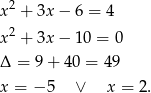
x2 + 3x− 6 = 4 x2 + 3x− 10 = 0 Δ = 9 + 40 = 49 x = − 5 ∨ x = 2.

Jest jasne, że obie liczby są rozwiązaniami danego równania (bo dla nich 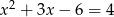x 2 + 3x − 6 = 4 ).  
Odpowiedź: 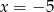x = − 5 lub x = 2

Wersja PDF