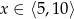Zadanie nr 1963037
Rozwiąż równanie 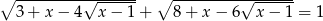 .
.
Rozwiązanie
Sposób I
Zanim zajmiemy się dziedziną równania, spróbujmy je przekształcić.
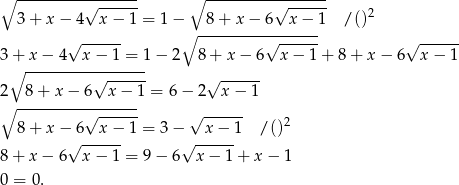
Tak więc równanie jest zawsze spełnione, o ile ma sens, i o ile powyższe przejścia były równoważnościami (jeżeli podnosiliśmy równanie do kwadratu, to strony musiały być nieujemne). Sprawdźmy najpierw jaka jest dziedzina równania.
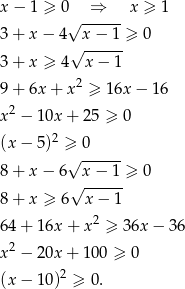
Zatem dziedziną równania jest zbiór 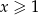 .
.
Pozostało sprawdzić kiedy
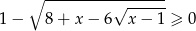
i
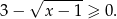
Liczymy
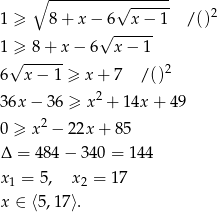
Druga nierówność
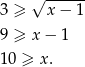
Sposób II
Jeżeli dokładnie popatrzymy na poprzednie rozwiązanie, to można zauważyć, że
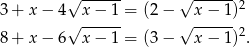
Podane równanie możemy więc zapisać w postaci
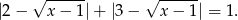
Jak zwykle w tego typu równaniu, mamy trzy przypadki
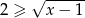 , czyli
, czyli 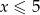 . Mamy wtedy równanie
. Mamy wtedy równanie
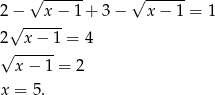
Jeżeli 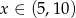 , to mamy tożsamościowe równanie
, to mamy tożsamościowe równanie
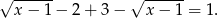
Jeżeli natomiast 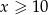 to mamy
to mamy
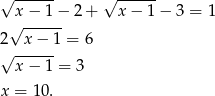
Sposób III
Tak jak poprzednio zauważamy, że
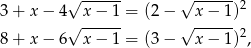
co daje nam równanie
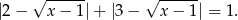
Tym razem jednak, zamiast rozważać przypadki, skorzystajmy z interpretacji geometrycznej wyrażenia 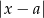 – jest dokładnie odległość
– jest dokładnie odległość  od
od  . Powyższe równanie jest zatem zapisem tego, że suma odległości
. Powyższe równanie jest zatem zapisem tego, że suma odległości 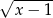 od 2 i od 3 jest równa 1. Gdy sobie to naszkicujemy, to jest jasne, że tak będzie dokładnie wtedy gdy
od 2 i od 3 jest równa 1. Gdy sobie to naszkicujemy, to jest jasne, że tak będzie dokładnie wtedy gdy 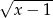 jest w przedziale
jest w przedziale 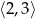 (na zewnątrz tego przedziału suma odległości jest większa od 1, a w środku jest to dokładnie odległość między 2 i 3). Mamy zatem
(na zewnątrz tego przedziału suma odległości jest większa od 1, a w środku jest to dokładnie odległość między 2 i 3). Mamy zatem
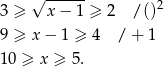
Sposób IV
Podstawmy 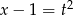 (możemy tak podstawić, bo
(możemy tak podstawić, bo 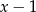 jest pod pierwiastkiem, więc musi być
jest pod pierwiastkiem, więc musi być 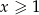 ). Załóżmy ponadto, że
). Załóżmy ponadto, że 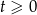 . Wtedy
. Wtedy 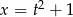 i otrzymujemy równanie
i otrzymujemy równanie
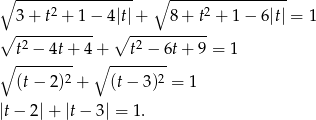
Rozważmy teraz przypadki.
Jeżeli 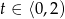 to mamy
to mamy
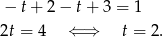
Założyliśmy jednak, że 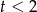 , więc w tym przypadku nie ma rozwiązań.
, więc w tym przypadku nie ma rozwiązań.
Jeżeli 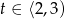 to mamy
to mamy
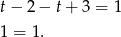
Mamy więc w tym przypadku 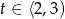 .
.
W końcu, jeżeli 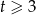 to mamy
to mamy
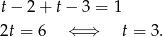
Zbierając razem wszystkie przypadki mamy więc 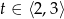 . Pozostało wyliczyć
. Pozostało wyliczyć  .
.
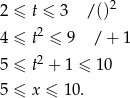
Odpowiedź: