Zadanie nr 3225505
Funkcja 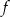 ma następujące własności:
ma następujące własności:
1. Dziedziną funkcji jest przedział 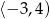 .
.
2. Przedział 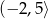 jest zbiorem wartości funkcji
jest zbiorem wartości funkcji 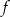 .
.
3. Funkcja ma dwa miejsca zerowe -2 oraz 3.
4. Funkcja 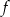 jest rosnąca w przedziale
jest rosnąca w przedziale 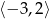 i malejąca w przedziale
i malejąca w przedziale 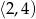 . Podaj zbiór rozwiązań nierówności
. Podaj zbiór rozwiązań nierówności 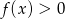 .
.
Rozwiązanie
Wiemy, że funkcja 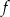 rośnie na przedziale
rośnie na przedziale 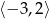 oraz przecina oś
oraz przecina oś 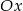 dla
dla 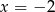 . To oznacza, że na przedziale
. To oznacza, że na przedziale 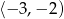 jej wykres znajduje się poniżej osi
jej wykres znajduje się poniżej osi 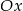 , a na przedziale
, a na przedziale 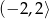 jej wykres jest powyżej osi
jej wykres jest powyżej osi 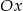 .
.
Podobnie, ponieważ funkcja maleje na przedziale 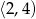 i ma miejsce zerowe
i ma miejsce zerowe 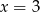 , wykres jest powyżej osi
, wykres jest powyżej osi 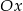 dla
dla 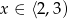 i poniżej osi
i poniżej osi 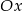 dla
dla 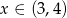 . Rozwiązaniem nierówności
. Rozwiązaniem nierówności 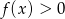 jest więc zbiór
jest więc zbiór
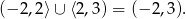
Na koniec przykładowy wykres funkcji 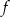 .
.
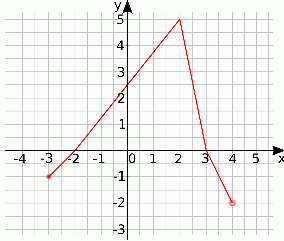
Odpowiedź: