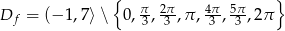Zadanie nr 3911884

Wyznaczyć dziedzinę funkcji 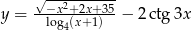√-−x2+2x+35- y = log4(x+1) − 2 ctg 3x .

Rozwiązanie

Ze względu na logarytm musi być

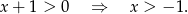
x + 1 > 0 ⇒ x > − 1.

Ze względu na mianownik musi być

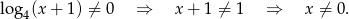
log4(x + 1) ⁄= 0 ⇒ x + 1 ⁄= 1 ⇒ x ⁄= 0.

Ze względu na cotangens

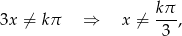
3x ⁄= kπ ⇒ x ⁄= kπ-, 3

gdzie 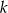dowolna liczba całkowita. Zauważmy, że dla 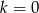k = 0 mamy poprzedni warunek: x ⁄= 0 .

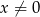Pozostało sprawdzić kiedy wyrażenie pod pierwiastkiem jest nieujemne.

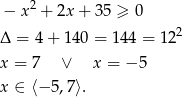
− x2 + 2x + 3 5 ≥ 0 2 Δ = 4 + 140 = 144 = 12 x = 7 ∨ x = −5 x ∈ ⟨−5 ,7⟩.

Łącząc wszystkie usyskane warunki mamy

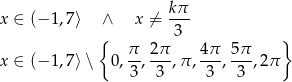
x ∈ (− 1,7⟩ ∧ x ⁄= kπ- { 3 } π- 2π- 4π- 5π- x ∈ (− 1,7⟩∖ 0,3 , 3 ,π , 3 , 3 ,2π

Odpowiedź: { π- 2π- 4π- 5π-- } Df = (− 1,7⟩ ∖ 0,3 , 3 ,π , 3 , 3 ,2π

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz