Z trzech prostopadłościennych belek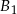 
, 
, 
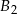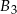o takich samych przekrojach poprzecznych i długościach odpowiednio równych 1 m, 2 m, 1 m sklejono jedną belkę o długości 4 m. Każda z belek 
, 
, 
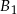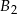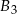wykonana jest z innego materiału, a ich masy są równe odpowiednio 20 kg, 30 kg, 10 kg.
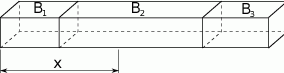
Masa odcinka belki o długosci 
jest funkcją zmiennej 
. Znajdź wzór tej funkcji.
Dopóki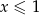 
, masa odcinka belki będzie proporcjonalna do 
, tzn.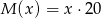 
. Jak zaczniemy poruszać się wzdłuż belki 
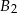, to masa będzie równa 
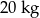(masa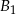 
) plus kawałek 
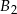długości 
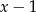, czyli
(
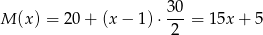
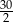to masa jednego metra belki 
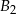). Podobnie jak poruszamy się wzdłuż 
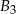, to mamy na niej odcinek długości 
.
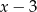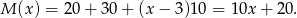
Zatem
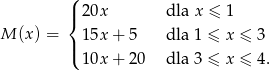
Odpowiedź: 
Informacje
Zadania
Losowe zadanie
