/Szkoła średnia/Funkcje/Różne

Zadanie nr 7966138

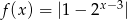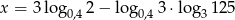Oblicz wartość funkcji x−3 f (x ) = |1− 2 | dla argumentu x = 3log0,42 − log0,4 3⋅ log 3125 .

Wersja PDF

Rozwiązanie

Uprośćmy najpierw podaną wartość x – logarytmy mają różne podstawy, więc sprowadźmy je wszystkie do wspólnej podstawy - w sumie wszystko jedno do jakiej, my zamieniamy wszystko na podstawę 5.

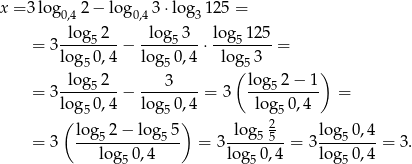
x = 3log0,42− lo g0,4 3⋅log 3125 = log 2 log 3 log 1 25 = 3----5---− ----5---⋅ ---5---- = log5 0,4 log5 0,4 log(5 3 ) log 2 3 lo g 2 − 1 = 3----5---− -------- = 3 ---5------ = log5 0,4 log5 0,4 lo g50,4 ( log 2− lo g 5 ) lo g5 2 log 0,4 = 3 ---5--------5-- = 3 ------5-= 3----5--- = 3. log 50,4 lo g50,4 log 50,4

Rachunek byłby jeszcze prostszy, gdybyśmy zmienili podstawę na 0,4:

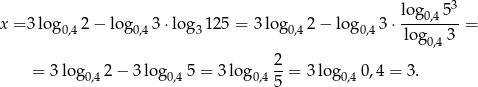
3 log0,4-5- x = 3 log 0,42 − log0,43 ⋅log31 25 = 3 log 0,42 − log0,43 ⋅ log 3 = 0,4 = 3 lo g 2− 3 log 5 = 3 lo g 2-= 3 lo g 0,4 = 3. 0,4 0,4 0,4 5 0,4

Liczymy zatem 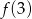f(3) .

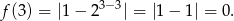
f(3) = |1 − 23− 3| = |1 − 1| = 0.

 
Odpowiedź: 0

Wersja PDF