/Szkoła średnia/Funkcje/Różne

Zadanie nr 8472459

Z równania 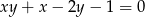xy+ x − 2y − 1 = 0 wyznacz 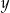y jako funkcję zmiennej x . Wyznacz jej dziedzinę oraz współrzędne punktów przecięcia wykresu z osiami układu współrzędnych.

Wersja PDF

Rozwiązanie

Rozpocznijmy od wyliczenia 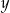y -ka.

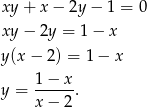
xy + x − 2y − 1 = 0 xy − 2y = 1− x y(x − 2) = 1− x y = 1−--x. x− 2

Dziedziną jest oczywiście zbiór 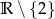R ∖ {2 } .

Punkty wspólne z osią 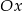Ox to miejsca zerowe, czyli (1,0) .

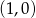Punkt wspólny z osią 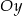Oy ma współrzędne 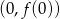(0,f(0)) . Ponieważ

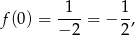
1 1 f(0) = −-2-= − 2-,

to jest to punkt 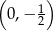( ) 0,− 1 2 .  
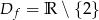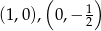Odpowiedź: Df = R ∖ {2 } , punkty wspólne z osiami ( ) 1 (1,0), 0,− 2 .

Wersja PDF