Zadanie nr 3833377
Funkcja 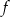 określona jest wzorem
określona jest wzorem 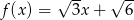 . Podaj miarę kąta ostrego, jaki tworzy wykres funkcji
. Podaj miarę kąta ostrego, jaki tworzy wykres funkcji 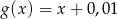 z prostą będącą wykresem funkcji
z prostą będącą wykresem funkcji 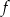 .
.
Rozwiązanie
Prosta 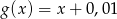 jest równoległa do prostej
jest równoległa do prostej 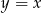 , a więc tworzy z osią
, a więc tworzy z osią 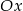 kąt
kąt 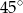 . Tangens kąta
. Tangens kąta  jaki tworzy z osią
jaki tworzy z osią 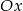 prosta
prosta 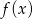 jest równy współczynnikowi kierunkowemu tej prostej, a więc
jest równy współczynnikowi kierunkowemu tej prostej, a więc
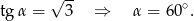
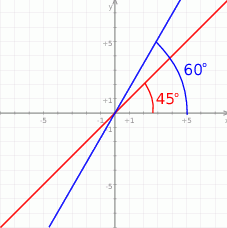
Zatem kąt przecięcia się podanych prostych to 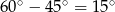 . Aby to dobrze widzieć, lepiej jest myśleć o prostej
. Aby to dobrze widzieć, lepiej jest myśleć o prostej 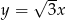 zamiast o
zamiast o 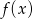 , bo przechodzi ona przez początek układ i jest równoległa do
, bo przechodzi ona przez początek układ i jest równoległa do 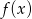 , więc tworzy z
, więc tworzy z 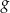 taki sam kąt.
taki sam kąt.
Odpowiedź: