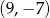Zadanie nr 9662919
Niech 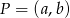 będzie dowolnym punktem wykresu funkcji
będzie dowolnym punktem wykresu funkcji 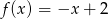 .
.
- Wyraź sumę odległości punktu
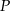 od osi układu współrzędnych jako funkcję zmiennej
od osi układu współrzędnych jako funkcję zmiennej  i naszkicuj wykres tej funkcji.
i naszkicuj wykres tej funkcji. - Znajdź współrzędne takiego punktu należącego do wykresu funkcji
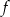 , którego suma odległości od osi układu współrzędnych jest równa 16.
, którego suma odległości od osi układu współrzędnych jest równa 16.
Rozwiązanie
- Odległości punktu
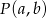 od osi
od osi 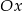 i
i 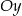 wynoszą odpowiednio
wynoszą odpowiednio 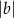 i
i 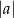 .
. 
Ponieważ punkt ten leży na prostej
 , mamy
, mamy 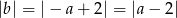 . Stąd suma jego odległości od osi wyraża się wzorem
. Stąd suma jego odległości od osi wyraża się wzorem 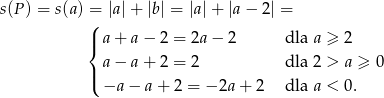
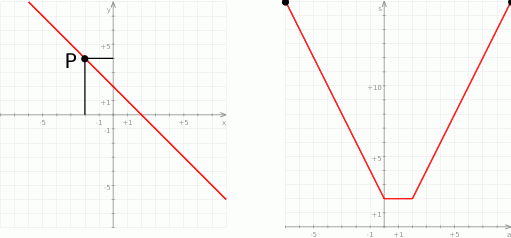
Teraz bez trudu rysujemy wykres funkcji
 .
.
Odpowiedź: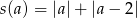
- Z wykresu (lub ze wzoru) z poprzedniego podpunktu odczytujemy, że
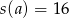 dla
dla 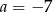 i
i 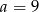 .
.
Odpowiedź: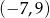 i
i