Zadanie nr 3483639
W ostrosłupie prawidłowym sześciokątnym pole przekroju płaszczyzną przechodzącą przez jego wysokość oraz przez dwie krawędzie boczne jest dwukrotnie większe od pola podstawy i wynosi 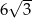 . Oblicz odległość spodka wysokości ostrosłupa od jego krawędzi bocznej.
. Oblicz odległość spodka wysokości ostrosłupa od jego krawędzi bocznej.
Rozwiązanie
Oczywiście najważniejszy jest rysunek.
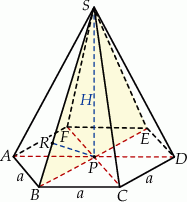
W podstawie ostrosłupa mamy 6 trójkątów równobocznych, oznaczmy długość ich boku przez  . Zatem pole podstawy to
. Zatem pole podstawy to
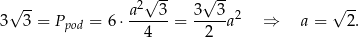
Mamy jeszcze informację o polu przekroju 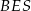 .
.
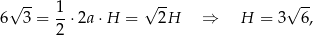
gdzie 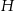 – wysokość ostrosłupa.
– wysokość ostrosłupa.
Szukana odległość to wysokość opuszczona na przeciwprostokątną w trójkącie prostokątnym 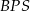 . Możemy ją obliczyć na różne sposoby, np. z podobieństwa trójkątów
. Możemy ją obliczyć na różne sposoby, np. z podobieństwa trójkątów 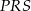 i
i 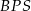 lub z porównania dwóch wzorów na pole trójkąta
lub z porównania dwóch wzorów na pole trójkąta 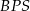 . My zrobimy to tą drugą metodą. Pole trójkąta
. My zrobimy to tą drugą metodą. Pole trójkąta 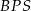 jest równe
jest równe
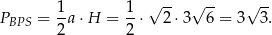
Policzmy jeszcze długość przeciwprostokątnej w tym trójkącie.
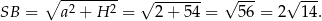
Mamy zatem
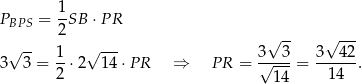
Odpowiedź: