/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy sześciokątny

Zadanie nr 4466400

Wysokość ostrosłupa prawidłowego sześciokątnego jest równa 6 cm i stanowi 32 długości krawędzi podstawy.

  • Oblicz miarę kąta nachylenia ściany bocznej do podstawy.
  • Oblicz objętość ostrosłupa
Wersja PDF

Rozwiązanie

Zaczynamy od rysunku

PIC

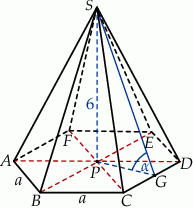
Obliczamy długość krawędzi podstawy

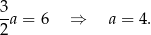
3a = 6 ⇒ a = 4. 2
  • Kąt nachylenia ściany bocznej do podstawy jest równy kątowi między wysokością ściany bocznej, a wysokością trójkąta w podstawie (patrz rysunek). Musimy jeszcze obliczyć długość odcinka P G
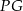
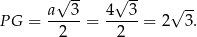
    √ -- √ -- √ -- PG = a--3-= 4--3-= 2 3 . 2 2

    Teraz możemy obliczyć kąt α

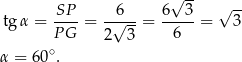
    √ -- √ -- tg α = -SP- = -√6--= 6--3-= 3 P G 2 3 6 α = 6 0∘.

     
    Odpowiedź: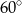 60∘

  • Obliczamy pole podstawy
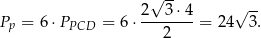
    √ -- -- P = 6 ⋅P = 6 ⋅ 2-3-⋅4-= 24√ 3. p PCD 2

    Teraz już łatwo obliczyć objętość

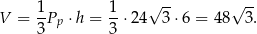
    1 1 √ -- √ -- V = -Pp ⋅h = --⋅24 3 ⋅6 = 48 3. 3 3

     
    Odpowiedź: √ -- 4 8 3 cm 3

Wersja PDF