Zadanie nr 8979525
W dwudziestościanie foremnym odcięto płaszczyznami przechodzącymi przez środki krawędzi każdy z narożników. Ile ścian ma powstała w ten sposób bryła i jakimi są one wielokątami?
Rozwiązanie
To co jest nam potrzebne do rozwiązania tego zadania, to wiedza, że dwudziestościan foremny ma ściany będące trójkątami równobocznymi, że w każdym wierzchołku spotyka się 5 krawędzi, i że jest 12 wierzchołków. W zasadzie nie jest potrzebny nawet rysunek, ale dla lepszej przejrzystości my go naszkicujemy.
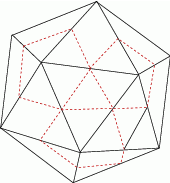
W obciętej bryle pozostaną wszystkie oryginalne ściany (choć będą przycięte) i dojdzie 12 nowych, pochodzących od odciętych naroży (tyle ile jest wierzchołków). Nowe ściany będą pięciokątami foremnymi, a stare ściany zostaną przycięte do trójkątów równobocznych (są to trójkąty o wierzchołkach w środkach krawędzi).
Odpowiedź: 32 ściany: 12 pięciokątów i 20 trójkątów foremnych.

