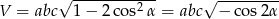Zadanie nr 9544562
Trzy wychodzące z jednego wierzchołka krawędzie równoległościanu są równe 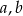 i
i  . Krawędzie
. Krawędzie  i
i 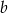 są prostopadłe, a krawędź
są prostopadłe, a krawędź  tworzy z każdą z nich kąt ostry
tworzy z każdą z nich kąt ostry  . Oblicz objętość równoległościanu.
. Oblicz objętość równoległościanu.
Rozwiązanie
Najtrudniejsza część tego zadania to wykonanie sensownego rysunku – i właśnie od tego zacznijmy.
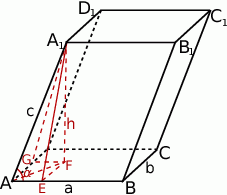
W podstawie równoległościanu mamy prostokąt o bokach  i
i 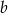 , więc przynajmniej jedna rzecz jest prosta: pole podstawy jest równe
, więc przynajmniej jedna rzecz jest prosta: pole podstawy jest równe
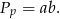
Do wyliczenia objętości brakuje nam więc długości wysokości – dorysujmy wysokość 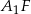 . Dorysujmy też wysokości ścian bocznych
. Dorysujmy też wysokości ścian bocznych 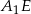 i
i 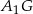 . Teraz powinno być już widać co dalej: wysokość możemy wyliczyć z trójkąta prostokątnego
. Teraz powinno być już widać co dalej: wysokość możemy wyliczyć z trójkąta prostokątnego 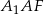 , a potrzebną do tego długość odcinka
, a potrzebną do tego długość odcinka 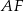 z trójkąta prostokątnego
z trójkąta prostokątnego 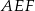 (czworokąt
(czworokąt 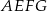 jest prostokątem, a tak naprawdę nawet kwadratem), a odcinki
jest prostokątem, a tak naprawdę nawet kwadratem), a odcinki 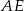 i
i 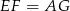 z trójkątów prostokątnych
z trójkątów prostokątnych 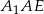 i
i 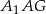 . Wszystko jasne, więc liczymy.
. Wszystko jasne, więc liczymy.
Z trójkątów prostokątnych 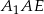 i
i 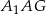 mamy
mamy
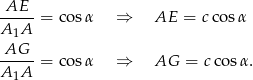
Teraz patrzymy na trójkąt prostokątny 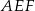 .
.
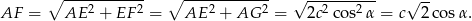
Teraz patrzymy na trójkąt prostokątny 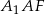 .
.
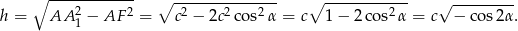
Wyrażenie pod pierwiastkiem jest dodatnie, bo łatwo sprawdzić, że 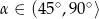 .
.
W takim razie objętość jest równa
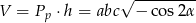
Odpowiedź: