/Szkoła średnia/Zadania z treścią/Procenty/Lokata

Zadanie nr 5972435

Dodaj do ulubionych
Dodaj do rozwiązanych

Pan Kowalski planując wyjazd na wakacje letnie w następnym roku postanowił założyć lokatę, wpłacając do banku 2000 zł na okres jednego roku. Ma do wyboru trzy rodzaje lokat:

  • lokata 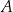A – oprocentowanie w stosunku rocznym 5%, kapitalizacja odsetek po roku;

  • lokata 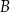B – oprocentowanie w stosunku rocznym 4,8%, kapitalizacja odsetek co pół roku;

  • lokata 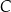C – oprocentowanie w stosunku rocznym 4,6%, kapitalizacja odsetek co kwartał.

Oceń, wykonując odpowiednie obliczenia, która lokata jest najkorzystniejsza dla Pana Kowalskiego.

Rozwiązanie

W wariancie 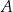A pan Kowalski otrzyma

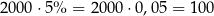
200 0⋅5% = 2000 ⋅0,05 = 10 0

złotych odsetek.

W wariancie 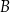B Pan Kowalski otrzyma po pierwszym pół roku

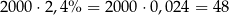
200 0⋅2,4 % = 2000 ⋅0,024 = 48

złotych odsetek. Ponadto, po drugiej połowie roku otrzyma dodatkowe

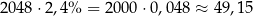
2048 ⋅2,4% = 2000 ⋅0,04 8 ≈ 49,15

złotych odsetek. Widać, że w sumie jest to miej niż 100 zł z wariantu 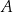A .

W wariancie 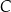C moglibyśmy liczyć jak przed chwilą, ale wygodniej jest skorzystać ze wzoru na procent składany.

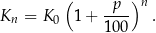
( ) K = K 1 + -p-- n. n 0 100

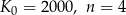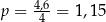W naszej sytuacji K0 = 2 000, n = 4 oraz p = 44,6-= 1,15 . Mamy więc

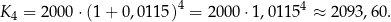
K = 2000 ⋅(1+ 0,0115)4 = 2000 ⋅1,01154 ≈ 2093,60. 4

Zatem najkorzystniejszy jest wariant 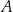A .  
Odpowiedź: Najkorzystniejszy jest wariant 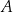A .

Wersja PDF