/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Nierówności z pierwiastkami

Zadanie nr 2705247

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz te wartości parametru 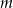m , dla których równanie 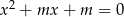2 x + mx + m = 0 ma takie dwa różne pierwiastki, że suma ich kwadratów jest mniejsza od 15.

Rozwiązanie

Sprawdźmy najpierw, kiedy równanie ma dwa pierwiastki.

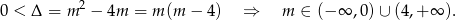
2 0 < Δ = m − 4m = m(m − 4) ⇒ m ∈ (− ∞ ,0) ∪ (4,+ ∞ ).

Skorzystamy teraz ze wzorów Viète’a

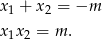
x1 + x2 = −m x1x2 = m .

Liczymy

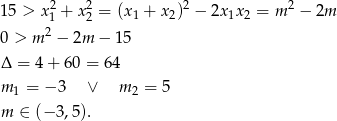
2 2 2 2 15 > x 1 + x 2 = (x1 + x2) − 2x1x2 = m − 2m 0 > m 2 − 2m − 15 Δ = 4+ 60 = 64 m 1 = − 3 ∨ m 2 = 5 m ∈ (− 3,5).

W połączeniu z warunkiem na 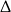Δ -ę mamy

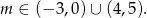
m ∈ (− 3,0)∪ (4,5).

 
Odpowiedź: m ∈ (− 3,0) ∪ (4,5)

Wersja PDF