/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Nierówności z pierwiastkami

Zadanie nr 3025216

Dodaj do ulubionych
Dodaj do rozwiązanych

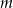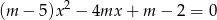Dla jakich wartości parametru m liczba 1 zawiera się między różnymi pierwiastkami równania (m − 5)x 2 − 4mx + m − 2 = 0 ?

Rozwiązanie

Wykres trójmianu 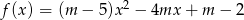2 f(x) = (m − 5)x − 4mx + m − 2 to parabola o ramionach skierowanych w górę dla 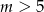m > 5 lub w dół dla 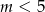m < 5 . W pierwszym przypadku podany warunek sprowadza się do tego, czy 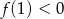f(1) < 0 (wtedy będą pierwiastki będą po różnych stronach 1-ki). W drugim przypadku musi być 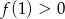f (1) > 0 . Sprawdzamy

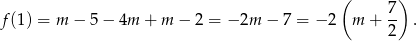
( ) 7 f (1) = m − 5− 4m + m − 2 = − 2m − 7 = − 2 m + -- . 2

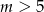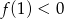Zatem dla m > 5 mamy f(1) < 0 . Natomiast dla 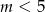m < 5 , musi być

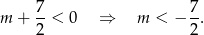
7 7 m + --< 0 ⇒ m < − -. 2 2

 
Odpowiedź: 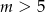m > 5 lub m < − 72

Wersja PDF