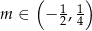/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Nierówności z pierwiastkami

Zadanie nr 3286319

Dodaj do ulubionych
Dodaj do rozwiązanych

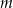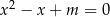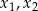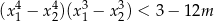Wyznacz wszystkie wartości parametru m , dla których równanie x 2 − x + m = 0 ma dwa rozwiązania rzeczywiste x 1,x 2 spełniające warunek (x41 − x24)(x 31 − x 32) < 3− 12m .

Rozwiązanie

Sprawdzamy najpierw, kiedy równanie ma dwa różne pierwiastki

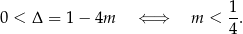
1 0 < Δ = 1 − 4m ⇐ ⇒ m < -. 4

Przy tym założeniu możemy napisać wzory Viète’a.

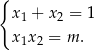
{ x1 + x2 = 1 x1x2 = m .

Spróbujemy teraz przekształcić lewą stronę podanej nierówności, tak aby móc skorzystać ze wzorów Viète’a. Zauważmy najpierw, że

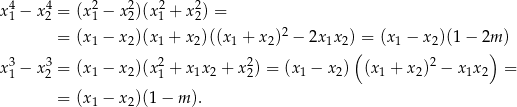
x 4− x 4= (x2− x2)(x2 + x2) = 1 2 1 2 1 2 = (x1 − x2)(x1 + x2)((x1 + x2)2 − 2x1x2) = (x1 − x2)(1− 2m ) 3 3 2 2 ( 2 ) x 1 − x 2 = (x1 − x2)(x1 + x1x2 + x2) = (x 1 − x 2) (x 1 + x 2) − x1x 2 = = (x1 − x2)(1− m ).

Stąd

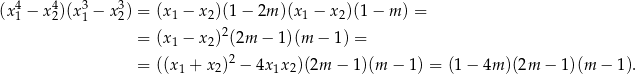
4 4 3 3 (x1 − x2)(x1 − x2) = (x 1 − x 2)(1 − 2m )(x 1 − x 2)(1− m ) = = (x 1 − x 2)2(2m − 1)(m − 1) = 2 = ((x 1 + x 2) − 4x 1x2)(2m − 1)(m − 1) = (1− 4m )(2m − 1)(m − 1).

Pozostało rozwiązać nierówność

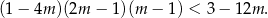
(1 − 4m )(2m − 1)(m − 1) < 3 − 12m .

Sposób I

Przekształcamy daną nierówność

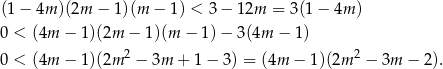
(1 − 4m )(2m − 1)(m − 1) < 3 − 12m = 3 (1− 4m ) 0 < (4m − 1)(2m − 1 )(m − 1) − 3(4m − 1) 0 < (4m − 1)(2m 2 − 3m + 1 − 3) = (4m − 1)(2m 2 − 3m − 2).

Rozkładamy teraz trójmian w drugim nawiasie.

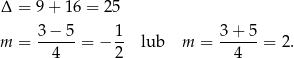
Δ = 9+ 16 = 25 3 − 5 1 3 + 5 m = ------= − -- lub m = ------= 2. 4 2 4

Mamy zatem nierówność

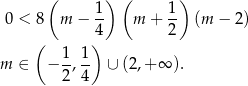
( ) ( ) 1 1 0 < 8 m − -- m + -- (m − 2) ( )4 2 1- 1- m ∈ − 2 ,4 ∪ (2,+ ∞ ).

W połączeniu z warunkiem na 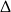Δ -ę mamy stąd

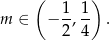
( ) 1- 1- m ∈ − 2, 4 .

Sposób II

Przekształcamy daną nierówność

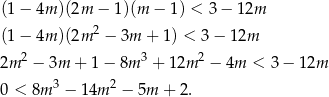
(1 − 4m )(2m − 1)(m − 1) < 3 − 12m 2 (1 − 4m )(2m − 3m + 1) < 3 − 12m 2m 2 − 3m + 1− 8m 3 + 12m 2 − 4m < 3− 1 2m 3 2 0 < 8m − 1 4m − 5m + 2.

Szukamy teraz pierwiastków wymiernych prawej strony – łatwo sprawdzić, że jednym z nich jest 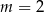m = 2 . Dzielimy teraz wielomian z prawej strony przez 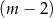(m − 2) – my zrobimy to grupując wyrazy.

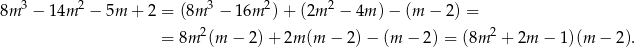
8m 3 − 14m 2 − 5m + 2 = (8m 3 − 16m 2) + (2m 2 − 4m )− (m − 2) = 2 2 = 8m (m − 2) + 2m (m − 2)− (m − 2) = (8m + 2m − 1)(m − 2).

Rozkładamy teraz trójmian w pierwszym nawiasie.

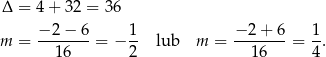
Δ = 4+ 3 2 = 36 m = −-2−--6 = − 1- lub m = −-2+--6 = 1-. 16 2 16 4

Mamy zatem nierówność

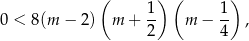
( 1) ( 1) 0 < 8(m − 2) m + -- m − -- , 2 4

którą rozwiązujemy dokładnie tak samo jak w pierwszym sposobie.  
Odpowiedź: ( ) m ∈ − 1 , 1 2 4

Wersja PDF