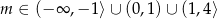Zadanie nr 4608865
Wyznacz wszystkie wartości parametru 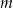 , dla których trójmian kwadratowy
, dla których trójmian kwadratowy
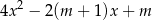
ma dwa różne pierwiastki rzeczywiste 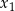 oraz
oraz 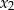 , spełniające warunki:
, spełniające warunki:
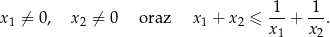
Rozwiązanie
Sprawdzamy najpierw, kiedy równanie ma dwa różne pierwiastki.
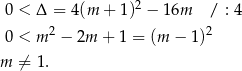
Wiemy ponadto, że rozwiązania mają być niezerowe, więc 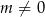 . Przy tych założeniach możemy skorzystać ze wzorów Viète’a
. Przy tych założeniach możemy skorzystać ze wzorów Viète’a
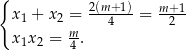
Przekształćmy nierówność, którą mamy rozwiązać.
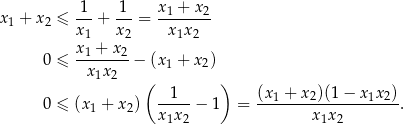
Korzystamy teraz z zapisanych wcześniej wzorów Viète’a
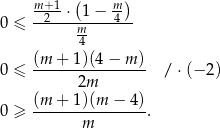
Przy założeniu 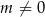 , nierówność ta jest równoważna nierówności wielomianowej
, nierówność ta jest równoważna nierówności wielomianowej
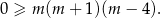
Zaznaczamy teraz miejsca zerowe prawej strony na osi.

Z rysunku odczytujemy rozwiązanie
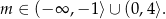
Z tego zbioru musimy jeszcze wyrzucić 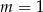 (z warunku z
(z warunku z 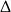 -ą), więc końcowa odpowiedź to
-ą), więc końcowa odpowiedź to
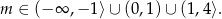
Odpowiedź: