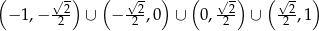/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Nierówności z pierwiastkami

Zadanie nr 5004831

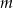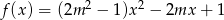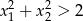Dla jakich wartości parametru m miejsca zerowe funkcji 2 2 f(x ) = (2m − 1)x − 2mx + 1 spełniają warunek x 21 + x 22 > 2 ?

Wersja PDF

Rozwiązanie

Po pierwsze musimy sprawdzić kiedy ta funkcja ma miejsca zerowe.

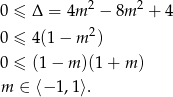
2 2 0 ≤ Δ = 4m − 8m + 4 0 ≤ 4 (1− m 2) 0 ≤ (1 − m )(1 + m ) m ∈ ⟨− 1,1⟩.

Wyrażenie 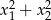x 2+ x 2 1 2 obliczymy ze wzorów Viéte’a.

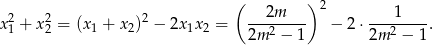
( ) 2 2 2 2m 2 1 x 1 + x 2 = (x1 + x2) − 2x1x2 = ---2---- − 2 ⋅---2----. 2m − 1 2m − 1

Mamy zatem nierówność

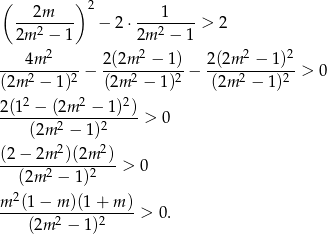
( ) --2m---- 2 ----1--- 2m 2 − 1 − 2 ⋅2m 2 − 1 > 2 2 2 2 2 ---4m------ 2(2m--−--1) 2(2m--−--1)- (2m 2 − 1 )2 − (2m 2 − 1)2 − (2m 2 − 1)2 > 0 2 2 2 2(1-−--(2m--−-1-)-)> 0 (2m 2 − 1 )2 2 2 (2−--2m--)(2m-)-> 0 (2m 2 − 1)2 m 2(1 − m )(1 + m ) -------2-----2-----> 0 . (2m − 1)

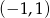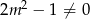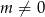Rozwiązaniem tej nierówności są wszystkie liczby z przedziału (− 1,1 ) , dla których 2 2m − 1 ⁄= 0 i m ⁄= 0 , czyli zbiór

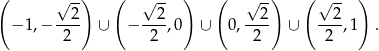
( √ -) ( √ -- ) ( √ -) ( √ -- ) − 1,− --2- ∪ − --2,0 ∪ 0 ,--2- ∪ --2,1 . 2 2 2 2

 
Odpowiedź: ( √2-) ( √-2 ) ( √-2) ( √2- ) − 1,− 2 ∪ − 2 ,0 ∪ 0, 2 ∪ 2 ,1

Wersja PDF