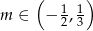/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Nierówności z pierwiastkami

Zadanie nr 5127525

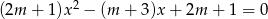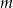Dane jest równanie 2 (2m + 1)x − (m + 3)x + 2m + 1 = 0 z niewiadomą x . Wyznacz te wartości parametru m , dla których suma odwrotności różnych pierwiastków danego równania jest większa od 1.

Wersja PDF

Rozwiązanie

Sprawdźmy najpierw kiedy równanie ma dwa różne pierwiastki. Oczywiście musi być kwadratowe, czyli 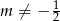m ⁄= − 12 oraz

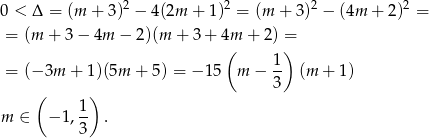
2 2 2 2 0 < Δ = (m + 3 ) − 4(2m + 1) = (m + 3) − (4m + 2) = = (m + 3 − 4m − 2)(m + 3+ 4m + 2) = ( ) = (− 3m + 1)(5m + 5 ) = − 15 m − 1- (m + 1) 3 ( 1 ) m ∈ − 1,-- . 3

Będziemy chcieli skorzystać ze wzorów Viète’a

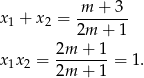
m-+--3- x1 + x2 = 2m + 1 2m + 1 x1x2 = ------- = 1. 2m + 1

Liczymy

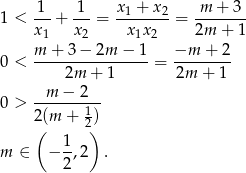
1 1 x1 + x2 m + 3 1 < --+ ---= --------= ------- x1 x2 x 1x 2 2m + 1 m-+-3-−-2m--−-1- −m--+-2- 0 < 2m + 1 = 2m + 1 m − 2 0 > -------1-- 2(m + 2) ( 1 ) m ∈ − -,2 . 2

W połączeniu z warunkiem na 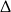Δ -ę otrzymujemy

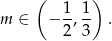
( 1 1) m ∈ − -, -- . 2 3

 
Odpowiedź: ( ) m ∈ − 12 , 13

Wersja PDF