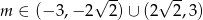/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Nierówności z pierwiastkami

Zadanie nr 5226060

Dodaj do ulubionych
Dodaj do rozwiązanych

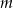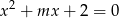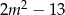Wyznacz wszystkie wartości parametru m , dla których równanie x 2 + mx + 2 = 0 ma dwa różne pierwiastki rzeczywiste takie, że suma ich kwadratów jest większa od 2m 2 − 13 .

Rozwiązanie

Sprawdźmy kiedy równanie ma dwa różne pierwiastki 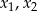x1,x2 .

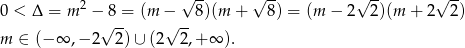
2 √ -- √ -- √ -- √ -- 0 < Δ = m −√8-= (m −√ --8)(m + 8) = (m − 2 2)(m + 2 2) m ∈ (− ∞ ,− 2 2)∪ (2 2,+ ∞ ).

Korzystamy teraz ze wzorów Viète’a

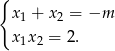
{ x1 + x2 = −m x x = 2. 1 2

Pozostało rozwiązać nierówność

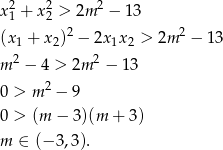
2 2 2 x1 + x2 > 2m − 13 (x1 + x2)2 − 2x1x2 > 2m 2 − 13 2 2 m − 4 > 2m − 13 0 > m 2 − 9 0 > (m − 3)(m + 3) m ∈ (− 3,3 ).

Ponieważ 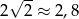√ -- 2 2 ≈ 2,8 w połączeniu z warunkiem na 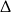Δ -ę daje to

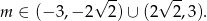
√ -- √ -- m ∈ (− 3 ,− 2 2)∪ (2 2 ,3 ).

 
Odpowiedź: √ -- √ -- m ∈ (− 3,− 2 2) ∪ (2 2,3)

Wersja PDF