Zadanie nr 7105849
Wyznacz te wartości parametru 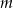 , dla których równanie
, dla których równanie 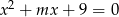 ma dwa rozwiązania mniejsze od
ma dwa rozwiązania mniejsze od 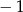 .
.
Rozwiązanie
Sprawdźmy najpierw kiedy podane równanie ma dwa rozwiązania.
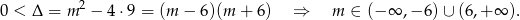
Sposób I
Rozwiązania będą mniejsze od 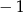 , jeżeli wierzchołek paraboli będącej wykresem podanego trójmianu będzie na lewo od
, jeżeli wierzchołek paraboli będącej wykresem podanego trójmianu będzie na lewo od 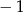 i wartość w
i wartość w 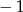 będzie dodatnia (bo warunki te gwarantują, że na prawo od
będzie dodatnia (bo warunki te gwarantują, że na prawo od 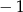 nie ma pierwiastków). Zatem
nie ma pierwiastków). Zatem
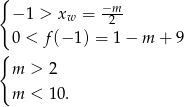
Łącząc wszystkie z otrzymanych warunków, mamy 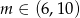 .
.
Sposób II
Wystarczy sprawdzić, kiedy większy z pierwiastków jest na lewo od 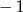 . Liczymy
. Liczymy
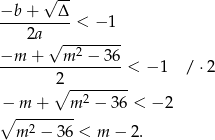
Chcielibyśmy teraz podnieść tę nierówność do kwadratu, ale aby móc to zrobić musimy założyć, że prawa strona jest nieujemna, czyli że 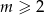 (jeżeli tak nie jest to nierówność jest sprzeczna).
(jeżeli tak nie jest to nierówność jest sprzeczna).
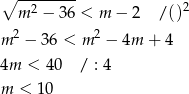
Łącząc wszystkie otrzymane warunki otrzymujemy rozwiązanie: 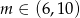 .
.
Sposób III
Jeżeli pierwiastki 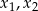 danego równania mają być mniejsze od
danego równania mają być mniejsze od 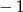 , to liczby
, to liczby 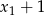 i
i 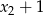 muszą być obie ujemne. Tak jest wtedy i tylko wtedy, gdy ich iloczyn jest dodatni, a suma ujemna.
muszą być obie ujemne. Tak jest wtedy i tylko wtedy, gdy ich iloczyn jest dodatni, a suma ujemna.
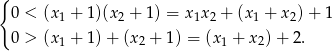
Korzystamy teraz ze wzorów Viète’a.
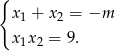
Musimy więc rozwiązać układ nierówności
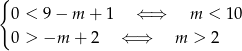
Łącząc wszystkie otrzymane warunki otrzymujemy rozwiązanie: 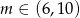 .
.
Sposób IV
Jeżeli ktoś nie boi się pochodnych, to warunek z treści zadania można zapisać jako 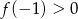 i
i 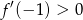 – funkcja ma być rosnąca w otoczeniu
– funkcja ma być rosnąca w otoczeniu 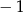 (czyli jesteśmy na prawej połówce paraboli). Warunek
(czyli jesteśmy na prawej połówce paraboli). Warunek 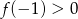 prowadzi do nierówności
prowadzi do nierówności

a warunek 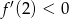 daje nam
daje nam
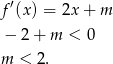
Łącząc wszystkie otrzymane warunki otrzymujemy rozwiązanie: 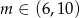 .
.
Odpowiedź: