/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Nierówności z pierwiastkami

Zadanie nr 8055883

Na płaszczyźnie z prostokątnym układem współrzędnych zilustruj zbiór wszystkich punktów płaszczyzny o współrzędnych 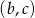(b,c) , takich, że równanie 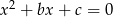x 2 + bx + c = 0 ma dwa różne rozwiązania należące do przedziału (1,+ ∞ ) .

Wersja PDF

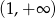Rozwiązanie

Zacznijmy od sprawdzenia, kiedy równanie ma dwa różne pierwiastki.

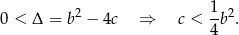
1 0 < Δ = b2 − 4c ⇒ c < --b2. 4

Sposób I

Kiedy oba pierwiastki będą większe od 1? Na pewno wierzchołek musi być na prawo od 1 (szkicujemy sobie to!), czyli

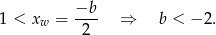
−b-- 1 < xw = 2 ⇒ b < − 2.

To jednak za mało, bo nadal mniejszy pierwiastek może być na lewo od 1. Aby tak nie były, wystarczy aby wartość w 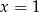x = 1 była nieujemna. Daje to nam

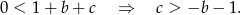
0 < 1+ b+ c ⇒ c > −b − 1.

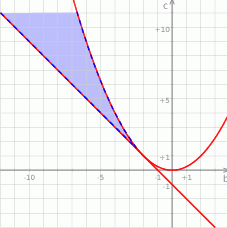
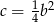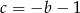Aby teraz naszkicować zbiór otrzymanych pary punktów, rysujemy wykresy funkcji 1 c = 4b2 oraz c = −b − 1 i zaznaczamy obszar pomiędzy nimi pamiętając, że ma być b < − 2 .

PIC

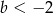Sposób II

Inny sposób ustalenia kiedy oba pierwiastki są większe od 1, to sprawdzenie kiedy mniejszy z nich jest większy od 1. Liczymy

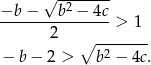
√ ------- −b − b2 − 4c ---------------> 1 2 ∘ ------- − b − 2 > b2 − 4c.

Widać teraz, że jeżeli lewa strona nie jest dodatnia, to nierówność jest sprzeczna. Mamy stąd 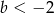b < − 2 . Przy tym założeniu obie strony są dodatnie i możemy nierówność podnieść stronami do kwadratu.

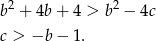
b2 + 4b + 4 > b2 − 4c c > −b − 1.

Obrazek wykonujemy jak w poprzednim sposobie.

Wersja PDF