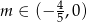/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Liczba pierwiastków

Zadanie nr 4357507

Dane jest równanie 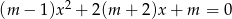2 (m − 1)x + 2(m + 2)x + m = 0 z niewiadomą x .

  • Zbadaj liczbę pierwiastków równania w zależności od wartości parametru m .
  • Dla jakich wartości parametru 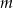m zachodzi nierówność 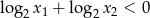log2 x1 + lo g2x 2 < 0 , gdzie 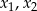x1,x2 są różnymi pierwiastkami danego równania.
Wersja PDF

Rozwiązanie

  • Sprawdźmy najpierw przypadek, gdy współczynnik przy 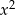x2 jest równy 0 (równanie nie jest kwadratowe). Dla 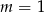m = 1 mamy równanie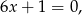
    6x + 1 = 0 ,

    które ma dokładnie jedno rozwiązanie.

    Jeżeli natomiast równanie jest kwadratowe, to liczymy 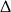Δ -ę.

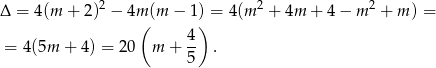
    2 2 2 Δ = 4(m + 2) − 4m((m − 1)) = 4(m + 4m + 4− m + m ) = 4 = 4(5m + 4) = 20 m + -- . 5

    Widzimy zatem, że liczba pierwiastków równania wyraża się wzorem

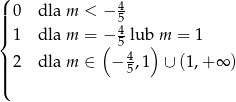
    ( 4 |||| 0 dla m < − 5 { 1 dla m = − 45 lub m = 1 ( 4 ) |||| 2 dla m ∈ − 5,1 ∪ (1,+ ∞ ) (
  • Aby wyrażenie
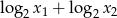
    log 2x1 + log2x 2

    miało sens oba pierwiastki równania muszą być dodatnie, oraz musi być spełniona nierówność

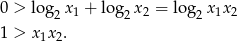
    0 > log 2x1 + log2 x2 = log2x 1x2 1 > x1x2.

    Oba te warunki (dodatniość pierwiastków i nierówność) możemy zapisać przy pomocy wzorów Viète’a następująco

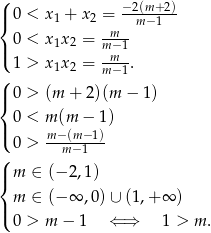
    ( −2(m+ 2) |{ 0 < x1 + x2 = --m−1--- 0 < x1x 2 = -m-- |( m−m-1 1 > x1x 2 = m− 1. (| 0 > (m + 2)(m − 1 ) { 0 < m (m − 1) |( 0 > m-−(m−-1) ( m −1 |{ m ∈ (−2 ,1) | m ∈ (−∞ ,0 )∪ (1,+ ∞ ) ( 0 > m − 1 ⇐ ⇒ 1 > m .

    Rozwiązaniem powyższego układu nierówności jest zbiór 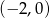(− 2,0) . W połączeniu z warunkiem na 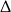Δ -ę z poprzedniego podpunktu daje to przedział (− 4,0) 5 .  
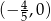    Odpowiedź: 4 m ∈ (− 5,0)

Wersja PDF