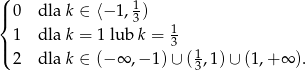/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Liczba pierwiastków

Zadanie nr 8880295

Określ liczbę pierwiastków równania 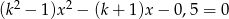2 2 (k − 1)x − (k+ 1)x− 0,5 = 0 w zależności od wartości parametru k .

Wersja PDF

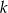Rozwiązanie

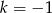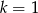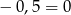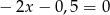Najpierw sprawdźmy co się dzieje jeżeli równanie jest liniowe, czyli dla k = −1 lub k = 1 . Mamy wtedy odpowiednio równania: − 0,5 = 0 i − 2x − 0,5 = 0 . Pierwsze z nich jest sprzeczne, drugie ma dokładnie jedno rozwiązanie.

Jeżeli równanie jest kwadratowe, to liczymy 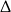Δ -ę.

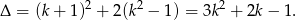
2 2 2 Δ = (k + 1 ) + 2(k − 1) = 3k + 2k − 1 .

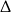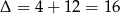Aby ustalić jaki jest znak Δ -y, musimy ten trójmian rozłożyć na czynniki: Δ = 4 + 12 = 1 6 , k1 = − 1 , 1 k2 = 3 . Zatem

( 1 |{ Δ > 0 dla k ∈ (− ∞ ,− 1)∪ (3 ,+ ∞ ) Δ = 0 dla k = − 1 lub k = 1 |( 1 3 Δ < 0 dla k ∈ (− 1,3).

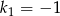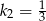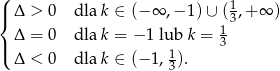
Zatem liczba rozwiązań równania wynosi (uwzględniamy sytuację gdy rówananie jest liniowe)

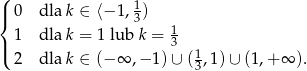
( |{ 0 dla k ∈ ⟨− 1, 13 ) 1 |( 1 dla k = 1 lub k = 3 2 dla k ∈ (− ∞ ,− 1) ∪ (13,1)∪ (1,+ ∞ ).

 
Odpowiedź: ( | 0 dla k ∈ ⟨− 1, 1) { 3 1 | 1 dla k = 1 lub k = 3 ( 2 dla k ∈ (− ∞ ,−1 )∪ (1,1) ∪ (1,+ ∞ ). 3

Wersja PDF