/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Liczba pierwiastków

Zadanie nr 9511350

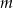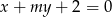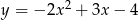Wyznacz wszystkie wartości parametru m , dla których prosta o równaniu x + my + 2 = 0 ma dokładnie dwa punkty wspólne z parabolą o równaniu y = − 2x2 + 3x − 4 .

Wersja PDF

Rozwiązanie

Sposób I

Jeżeli 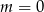m = 0 , to mamy prostą 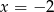x = − 2 i prosta ta ma tylko jeden punkt wspólny 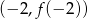(− 2,f (−2 )) z daną parabolą 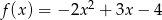f(x) = − 2x2 + 3x − 4 . Jeżeli natomiast 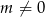m ⁄= 0 , to równanie danej prostej możemy zapisać w postaci 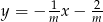y = − 1mx − m2 . Szukamy teraz punktów wspólnych tej prostej i danej paraboli (porównujemy 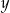y –ki).

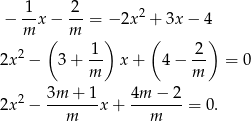
1 2 2 − --x − -- = − 2x + 3x − 4 m ( m ) ( ) 2x2 − 3+ 1- x + 4− 2- = 0 m m 3m + 1 4m − 2 2x2 − -------x + -------= 0. m m

Dana prosta i parabola mają dwa punkty wspólne wtedy i tylko wtedy, gdy powyższe równanie ma dwa rozwiązania, czyli gdy 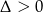Δ > 0 .

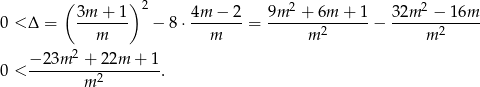
( )2 2 2 0 < Δ = 3m-+-1- − 8 ⋅ 4m-−-2 = 9m--+-6m--+-1-− 32m--−-1-6m- m m m 2 m 2 − 23m 2 + 22m + 1 0 < ------------------. m2

Pozostało więc rozwiązać nierówność kwadratową

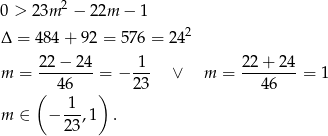
2 0 > 23m − 22m − 1 Δ = 48 4+ 92 = 576 = 242 m = 22−--24-= − 1-- ∨ m = 22+--24-= 1 ( 46 ) 23 46 1 m ∈ − ---,1 . 23

Na koniec trzeba pamiętać o wyrzuceniu 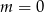m = 0 ze zbioru rozwiązań.

Sposób II

Podstawiamy 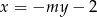x = −my − 2 z równania prostej do równania paraboli.

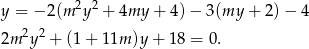
2 2 y = − 2(m y + 4my + 4) − 3(my + 2) − 4 2m 2y2 + (1+ 11m )y+ 18 = 0.

Dana prosta i parabola mają dwa punkty wspólne wtedy i tylko wtedy, gdy powyższe równanie ma dwa rozwiązania, czyli gdy 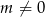m ⁄= 0 oraz

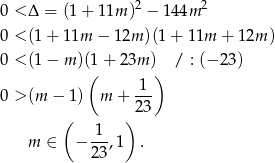
0 < Δ = (1+ 11m )2 − 1 44m 2 0 < (1+ 11m − 12m )(1+ 11m + 12m ) 0 < (1− m )(1+ 23m ) / : (− 23) ( ) 0 > (m − 1 ) m + 1-- 23 ( ) m ∈ − -1-,1 . 2 3

Na koniec trzeba pamiętać o wyrzuceniu 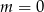m = 0 ze zbioru rozwiązań.  
Odpowiedź: ( ) m ∈ − 123,0 ∪ (0,1)

Wersja PDF