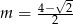/Szkoła średnia/Równania/Układy równań/Stopnia 2/Z parametrem

Zadanie nr 1698886

Dodaj do ul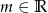ubionych
Dodaj do rozwiązanych

Dla jakich m ∈ R iloczyn pierwiastków układu równań

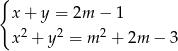
{ x + y = 2m − 1 x 2 + y 2 = m 2 + 2m − 3

przyjmuje wartość minimalną?

Rozwiązanie

Przekształcamy drugie równanie korzystając ze wzoru skróconego mnożenia na kwadrat sumy.

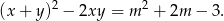
(x+ y)2 − 2xy = m 2 + 2m − 3.

Teraz podstawiamy 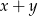x + y z pierwszego równania

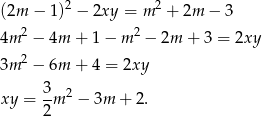
2 2 (2m − 1) − 2xy = m + 2m − 3 2 2 4m − 4m + 1− m − 2m + 3 = 2xy 3m 2 − 6m + 4 = 2xy xy = 3m 2 − 3m + 2. 2

Spróbujmy się teraz zastanowić dla jakich 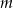m ten układ ma rozwiązanie. Na mocy wzorów Viète’a, rozwiązania tego układu są rozwiązaniami równania kwadratowego

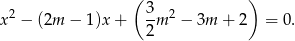
( ) 2 3- 2 x − (2m − 1)x+ 2m − 3m + 2 = 0 .

Sprawdźmy kiedy to równanie ma rozwiązania.

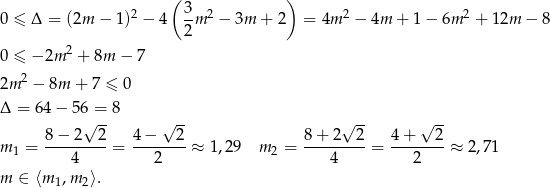
( 3 ) 0 ≤ Δ = (2m − 1)2 − 4 -m 2 − 3m + 2 = 4m 2 − 4m + 1 − 6m 2 + 12m − 8 2 0 ≤ − 2m 2 + 8m − 7 2 2m − 8m + 7 ≤ 0 Δ = 64− 56 = 8 √ -- √ -- √ -- √ -- 8-−-2--2- 4-−---2- 8-+-2--2- 4-+---2- m 1 = 4 = 2 ≈ 1 ,29 m 2 = 4 = 2 ≈ 2,71 m ∈ ⟨m1,m 2⟩.

Przypomnijmy sobie teraz, że mamy znaleźć najmniejszą wartość funkcji

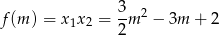
f(m ) = x x = 3m 2 − 3m + 2 1 2 2

Parabola będąca wykresem tej funkcji ma ramiona skierowane w górę, oraz wierzchołek w punkcie

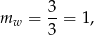
m = 3-= 1, w 3

więc najmniejszą wartość otrzymamy dla

√ -- 4−----2- m = 2

 
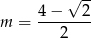
Odpowiedź: √- m = 4−--2 2

Wersja PDF