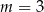Zadanie nr 9090479

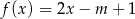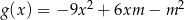Funkcje f(x) = 2x − m + 1 i 2 2 g (x) = − 9x + 6xm − m mają wspólne miejsce zerowe. Oblicz .

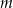Rozwiązanie

Sposób I

Zauważmy, że wzór funkcji 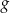to pełen kwadrat:

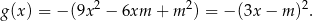
2 2 2 g (x) = − (9x − 6xm + m ) = − (3x − m ) .

To oznacza, że miejscem zerowym tej funkcji jest 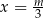m- x = 3 . Sprawdzamy teraz, kiedy jest to miejsce zerowe funkcji .

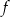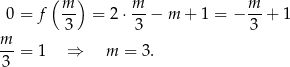
( m ) m m 0 = f -- = 2 ⋅-- − m + 1 = − -- + 1 3 3 3 m- = 1 ⇒ m = 3. 3

Sposób II

Wyznaczamy najpierw miejsce zerowe funkcji .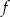

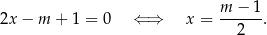
m-−-1- 2x− m + 1 = 0 ⇐ ⇒ x = 2 .

Sprawdzamy teraz, kiedy jest to też miejsce zerowe funkcji .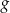

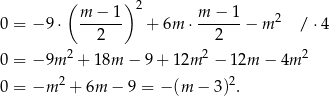
( ) m − 1 2 m − 1 2 0 = − 9⋅ ------ + 6m ⋅ ------− m / ⋅4 2 2 0 = − 9m 2 + 18m − 9 + 12m 2 − 12m − 4m 2 2 2 0 = −m + 6m − 9 = − (m − 3) .

Zatem 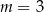m = 3 .
Odpowiedź: m = 3

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz