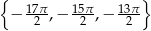Zadanie nr 9040433
Rozwiąż równanie 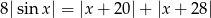 .
.
Rozwiązanie
Aby opuścić wartości bezwględne z prawej strony równania rozważamy trzy przypadki.
Jeżeli 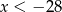 to wyrażenia pod każdą z wartości bezwzględnych są ujemne i mamy równanie
to wyrażenia pod każdą z wartości bezwzględnych są ujemne i mamy równanie
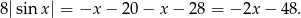
Zauważmy teraz, że z założenia 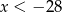 wynika, że
wynika, że
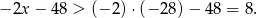
To oznacza, że równanie jest sprzeczne, bo lewa strona równania nie może być większa niż 8.
Jeżeli 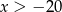 to wyrażenia pod obiema wartościami bezwzględnymi są dodatnie i mamy równanie
to wyrażenia pod obiema wartościami bezwzględnymi są dodatnie i mamy równanie
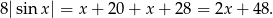
Z założenia 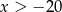 mamy
mamy
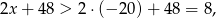
więc tak jak poprzednio równanie jest sprzeczne.
Jeżeli wreszcie 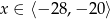 to mamy równanie
to mamy równanie
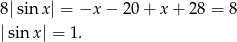
Rozwiązaniami tego równania są liczby 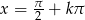 , gdzie
, gdzie 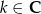 , ale nie możemy zapomnieć o warunku
, ale nie możemy zapomnieć o warunku 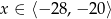 . Sprawdzamy na kalkulatorze, że
. Sprawdzamy na kalkulatorze, że
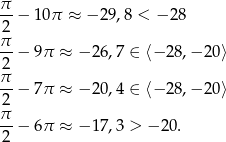
Równanie ma więc trzy rozwiązania:
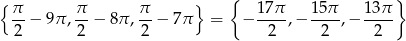
Odpowiedź: