/Szkoła średnia/Równania/Z wartością bezwględną/Trygonometryczne

Zadanie nr 9089710

Rozwiąż równanie: 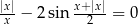|x|- x+|x| x − 2sin 2 = 0 .

Wersja PDF

Rozwiązanie

Oczywiście musi być 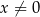x ⁄= 0 . Rozważamy dwa przypadki.

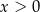  • x > 0 . Mamy wtedy równanie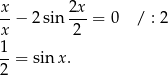
    x-− 2 sin 2x-= 0 / : 2 x 2 1 --= sin x. 2

    Rozwiązaniem tego równania są liczby postaci

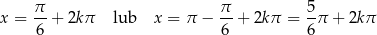
    x = π- + 2kπ lub x = π − π-+ 2kπ = 5π + 2kπ 6 6 6

    Pamiętajmy jednak, że ma być 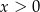x > 0 , co oznacza, że k ≥ 0 .

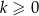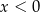  • x < 0 . Mamy wtedy równanie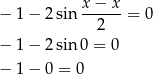
    x− x − 1− 2 sin ------= 0 2 − 1− 2 sin0 = 0 − 1− 0 = 0

    Równanie w tym przypadku jest więc sprzeczne.

 
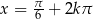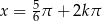Odpowiedź: x = π-+ 2kπ 6 lub x = 5π + 2kπ 6 dla k ∈ N ∪ {0}

Wersja PDF