Zadanie nr 3004505
Rozwiąż równanie 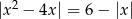 .
.
Rozwiązanie
Zapiszmy równanie w postaci
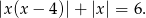
Wyrażanie pod pierwszą wartością bezwzględną jest dodatnie dla 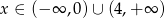 . Mamy zatem 3 przypadki.
. Mamy zatem 3 przypadki.
Jeżeli 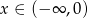 , to mamy równanie
, to mamy równanie
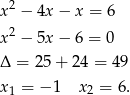
Tylko pierwsze z tych rozwiązań jest w przedziale 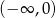 .
.
Jeżeli 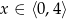 to
to
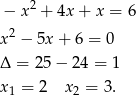
Jeżeli 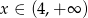 to
to
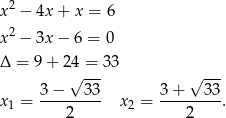
Tylko druga z tych liczb jest w przedziale 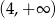 .
.
Odpowiedź: