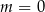Zadania.info
Największy internetowy zbiór zadań z matematyki
cornersUpL
cornersUpR

Zadania

Na skróty

Recenzje

Linki sponsorowane

cornersM
Zaloguj się

Linki sponsorowane

cornersR
Zadanie nr 1147099

Wyznacz te wartości parametru 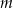m , dla których równanie 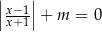||x−1|| |x+1|+ m = 0 z niewiadomą x ma dokładnie jedno rozwiązanie.

Wersja PDF
Rozwiązanie

Przekształćmy odrobinę równanie tak, aby miało prostszą postać.

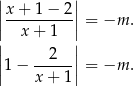
||x + 1− 2|| ||---------|| = −m . | x + 1 | | 2 | ||1− x+--1|| = −m .

Sposób I

Możemy narysować wykres lewej strony równania – zaczynamy od hiperboli 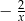2 − x , przesuwamy ją o 1 jednostkę w górę i 1 jednostkę w lewo, następnie odbijamy część poniżej osi 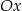Ox do góry.

PIC

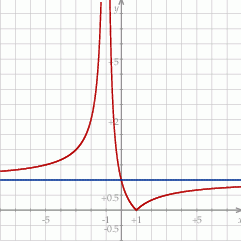
Z tego wykresu łatwo odczytać, że równanie ma dokładnie jedno rozwiązanie wtedy i tylko wtedy, gdy 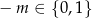− m ∈ {0,1} , czyli m ∈ {− 1,0} .

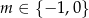Sposób II

Po pierwsze, jeżeli 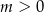m > 0 to równanie to nie ma rozwiązań. Jest też jasne, że jeżeli 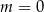m = 0 , to to jedynym rozwiązaniem równania jest 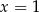x = 1 . Załóżmy więc, że 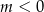m < 0 . Wtedy równanie jest równoważne dwóm równaniom

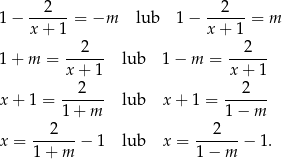
2 2 1 − ------= −m lub 1− ------= m x+ 1 x + 1 1 + m = --2--- lub 1 − m = --2--- x+ 1 x + 1 2 2 x + 1 = 1-+-m- lub x + 1 = 1−-m-- x = --2--- − 1 lub x = --2---− 1 . 1 + m 1− m

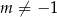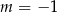Powyższy rachunek ma oczywiście sens tylko jeżeli m ⁄= − 1 . Dla m = − 1 lewe równanie jest sprzeczne, więc interesujące nas równanie ma jedno rozwiązanie.

Sprawdźmy jeszcze tylko, czy otrzymane wyżej pierwiastki mogą być równe

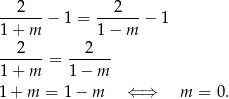
2 2 ------ − 1 = ------− 1 1 + m 1− m ---2-- = --2--- 1 + m 1− m 1 + m = 1 − m ⇐ ⇒ m = 0.

 
Odpowiedź: 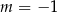m = − 1 lub m = 0

Wersja PDF
Twoje uwagi
Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!