/Szkoła średnia/Równania/Z wartością bezwględną/Wymierne/Z parametrem

Zadanie nr 3939388

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 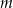m równanie 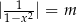--1- |1−x2| = m ma trzy rozwiązania?

Rozwiązanie

Aby równanie w ogóle miało rozwiązania musi być 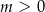m > 0 . Równanie to jest równoważne dwóm równaniom.

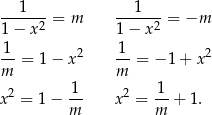
--1----= m ---1---= −m 1− x 2 1 − x 2 1- 2 -1 2 m = 1− x m = −1 + x 1 1 x 2 = 1− -- x2 = --+ 1. m m

Zauważmy, że drugie z tych równań ma zawsze dwa rozwiązania (dla 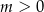m > 0 ). Ponadto 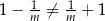1 1 1 − m- ⁄= m-+ 1 , więc rozwiązania tego równania nie mogą być rozwiązaniami pierwszego równania. Zatem, wyjściowe równanie ma dokładnie trzy rozwiązania tylko wtedy, gdy równanie 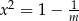x2 = 1− 1- m ma jedno rozwiązanie, czyli dla m = 1 .

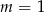Dla ciekawskich wykres funkcji 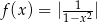-1-- f(x ) = |1−x2| .

PIC

 
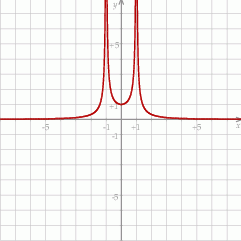
Odpowiedź: m = 1

Wersja PDF