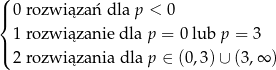Zadanie nr 9969883

Dane jest równanie 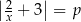||2 || x + 3 = p z niewiadomą . Wyznacz liczbę rozwiązań tego równania w zależności od parametru .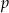

Rozwiązanie

Sposób I

Możemy narysować wykres lewej strony równania – jest to hiperbola 2 x przesunięta o 3 jednostki w górę i część poniżej osi jest zagięta do góry.

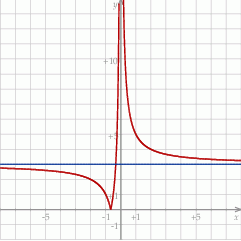
Z tego wykresu łatwo odczytujemy liczbę jego punktów przecięcia z prostą 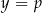y = p .

Sposób II

Po pierwsze, jeżeli 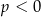p < 0 to równanie to nie ma rozwiązań. Jeżeli natomiast 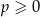p ≥ 0 , to równanie to jest równoważne dwóm równaniom

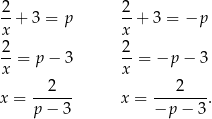
2 2 -+ 3 = p --+ 3 = −p x x 2-= p − 3 2-= −p − 3 x x --2--- ---2---- x = p − 3 x = −p − 3.

Widać więc, że maksymalnie są dwa rozwiązania. Pozostało sprawdzić, co się dzieje dla 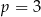p = 3 i kiedy te dwa rozwiązania są równe.

Dla 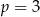p = 3 dwa pierwsze z równań nie ma rozwiązania (bo jest postaci 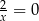x2= 0 ), zatem wyjściowe równanie ma jedno rozwiązanie.

Sprawdźmy jescze kiedy dwa rozwiązania są równe

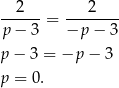
--2--- ---2---- p − 3 = −p − 3 p− 3 = −p − 3 p = 0.

Zatem wyjściowe równanie ma

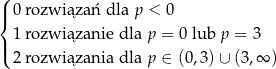
( | 0 rozwi ązań dla p < 0 { | 1 rozwi ązanie dla p = 0 lub p = 3 ( 2 rozwi ązania dla p ∈ (0,3) ∪ (3,∞ )

Odpowiedź: ( |{ 0 rozwi ązań dla p < 0 1 rozwi ązanie dla p = 0 lub p = 3 |( 2 rozwi ązania dla p ∈ (0,3) ∪ (3,∞ )