/Gimnazjum/Egzamin gimnazjalny
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 1 kwietnia 2017 Czas pracy: 90 minut
Informacja do zadań 1 i 2
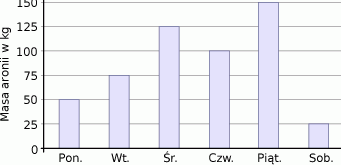
Pan Łukasz przez sześć kolejnych dni tygodnia pracował przy zbiórce aronii. Na diagramie przedstawiono wyniki jego zbiorów.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Z informacji podanych na diagramie wynika, że pan Łukasz
A) w czwartek zebrał więcej aronii niż w kolejnym dniu.
B) w ciągu pierwszych trzech dni zebrał tyle samo aronii, co w ciągu trzech kolejnych dni.
C) w poniedziałek zebrał trzy razy więcej aronii niż w sobotę.
D) w sobotę zebrał trzy razy mniej aronii niż we wtorek.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Pan Łukasz zbierał średnio 85 kg aronii dziennie. | P | F |
| Gdyby pan Łukasz w sobotę zebrał dwa razy więcej owoców, to w sumie zebrałby 550 kg aronii. | P | F |
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Odległość między punktami, które na osi liczbowej odpowiadają liczbom 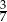 i
i 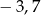 jest równa
jest równa
A) 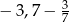 B)
B) 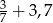 C)
C) 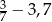 D)
D) 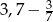
Dane są liczby
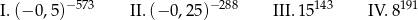
Która z tych liczb jest największa? Wybierz właściwą odpowiedź spośród podanych.
A) I B) II C) III D) IV
Ile jest liczb dwucyfrowych parzystych, które przy dzieleniu przez 9 dają resztę 2 i jednocześnie są podzielne przez 7?
A) 1 B) 2 C) 3 D) 4
W tabeli podano, w jaki sposób zmienia się cena biletu na górskim wyciągu linowym w ciągu całego roku.
| Cena podstawowa biletu na wyciąg | 50 zł |
| Cena biletu w sezonie zimowym | cena podstawowa podwyższona o 140% |
| Cena biletu w sezonie letnim | cena podstawowa obniżona o 30% |
| Cena biletu poza sezonem zimowym i letnim | cena podstawowa |
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Bilet na wyciąg w sezonie letnim jest tańszy od biletu w sezonie zimowym o
A) 70 zł B) 15 zł C) 85 zł D) 55 zł
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba 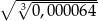 jest równa
jest równa
A) 0,02 B) 0,2 C) 0,04 D) 0,08
Na wycieczkę szkolną pojechali uczniowie dwóch klas: klasy IIa i IIb. Liczba uczniów klasy IIa stanowi  liczby uczniów klasy IIb. Ponadto
liczby uczniów klasy IIb. Ponadto  uczniów każdej z klas stanowią dziewczęta. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
uczniów każdej z klas stanowią dziewczęta. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Na wycieczkę pojechało dwa razy więcej dziewcząt niż chłopców. | P | F |
| Na wycieczkę pojechało 3 razy więcej uczniów klasy IIb niż klasy IIa. | P | F |
Na ulicznym straganie z kwiatami sprzedano tyle samo róż, co tulipanów oraz 16 goździków. Goździki stanowiły 12,5% liczby sprzedanych kwiatów. Ile tulipanów sprzedano na straganie? Wybierz odpowiedź spośród podanych.
A) 56 B) 28 C) 64 D) 112
Jeżeli odcinek 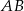 podzielimy na 80 równych części, to każda część ma długość 0,15 cm. Który wzór opisuje zależność między liczbą równych części (
podzielimy na 80 równych części, to każda część ma długość 0,15 cm. Który wzór opisuje zależność między liczbą równych części ( ), na którą dzielimy odcinek
), na którą dzielimy odcinek 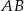 , a długością (
, a długością (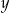 ) jednej takiej części w milimetrach?
) jednej takiej części w milimetrach?
Wybierz właściwą odpowiedź spośród podanych.
A) 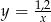 B)
B) 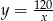 C)
C) 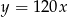 D)
D) 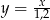
W układzie współrzędnych narysowano trójkąt równoboczny tak, że jednym z jego wierzchołków jest punkt 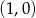 , jeden z wierzchołków jest na osi
, jeden z wierzchołków jest na osi 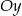 , a jeden z jego boków jest równoległy do osi
, a jeden z jego boków jest równoległy do osi 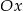 (zobacz rysunek).
(zobacz rysunek).
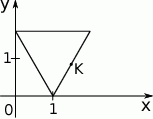
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Współrzędne środka 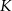 boku trójkąta są równe
boku trójkąta są równe
A) 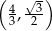 B)
B) 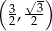 C)
C) 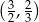 D)
D) 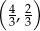
W układzie współrzędnych narysowano trójkąt równoboczny tak, że jednym z jego wierzchołków jest punkt 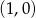 , jeden z wierzchołków jest na osi
, jeden z wierzchołków jest na osi 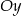 , a jeden z jego boków jest równoległy do osi
, a jeden z jego boków jest równoległy do osi 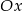 . Do tego trójkąta dorysowujemy kolejne takie same trójkąty. Umieszczamy je tak, jak na rysunku, aby każdy następny trójkąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego trójkąta był równoległy do osi
. Do tego trójkąta dorysowujemy kolejne takie same trójkąty. Umieszczamy je tak, jak na rysunku, aby każdy następny trójkąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego trójkąta był równoległy do osi 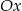 . Poniżej przedstawiono dorysowane, zgodnie z tą regułą, trójkąty, które ponumerowano kolejnymi liczbami naturalnymi.
. Poniżej przedstawiono dorysowane, zgodnie z tą regułą, trójkąty, które ponumerowano kolejnymi liczbami naturalnymi.
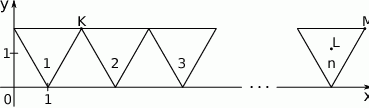
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Środek 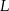 w w  –tym trójkącie ma współrzędne –tym trójkącie ma współrzędne 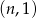 . . | P | F |
Wierzchołek 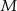 w w  –tym trójkącie ma współrzędne –tym trójkącie ma współrzędne 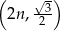 . . | P | F |
Maszyna produkcyjna wytwarza codziennie tę samą liczbę elementów. Wykonanie pewnego zamówienia wymaga jednoczesnej pracy pewnej liczby takich maszyn przez 15 dni. Gdyby jednak zwiększyć liczbę pracujących maszyn o 4, to czas wykonania zamówienia skróciłby się o 2 dni.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczbę maszyn potrzebnych do realizacji zamówienia można obliczyć, rozwiązując równanie
A) 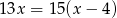 B)
B) 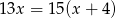 C)
C) 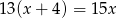 D)
D) 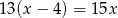
Słoń indyjski osiąga masę od 3,5 do 5 ton i zjada dziennie około 150 kg pokarmu. Na ile co najmniej dni wystarczy 5 ton pokarmu dla 4 słoni indyjskich?
Wybierz właściwą odpowiedź spośród podanych.
A) 8 B) 9 C) 33 D) 34
Na rysunku przedstawiono siatkę nietypowej sześciennej kostki do gry. Rzucamy jeden raz taką kostką.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyrzucenia nieparzystej liczby oczek jest 2 razy większe niż prawdopodobieństwo wyrzucenia parzystej liczby oczek. | P | F |
Prawdopodobieństwo wyrzucenia liczby oczek mniejszej od 3 jest równe  . . | P | F |
Jeden z kątów trójkąta prostokątnego 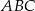 ma miarę
ma miarę 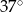 . Trójkąt
. Trójkąt 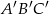 jest podobny do trójkąta
jest podobny do trójkąta 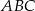 w skali 2:1.
w skali 2:1.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Miara najmniejszego kąta trójkąta 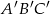 jest równa
jest równa
A) 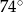 B)
B) 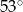 C)
C) 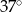 D)
D) 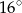
Punkty 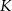 ,
, 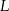 i
i 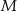 są środkami boków
są środkami boków 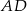 ,
, 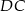 i
i 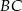 kwadratu
kwadratu 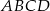 (rysunek).
(rysunek).
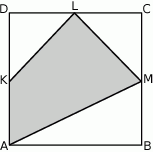
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta 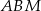 stanowi stanowi  pola kwadratu pola kwadratu 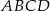 . . | P | F |
Pole czworokąta 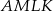 stanowi połowę pola kwadratu stanowi połowę pola kwadratu 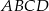 . . | P | F |
Każdy bok pięciokąta foremnego 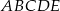 podzielono na 3 równe części i połączono kolejno punkty podziału, w wyniku czego otrzymano dziesięciokąt (rysunek).
podzielono na 3 równe części i połączono kolejno punkty podziału, w wyniku czego otrzymano dziesięciokąt (rysunek).
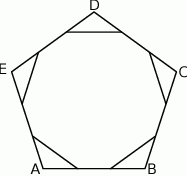
Które z poniższych zdań jest prawdziwe? Wybierz właściwą odpowiedź spośród podanych.
A) Dziesięciokąt jest foremny.
B) Wszystkie boki dziesięciokąta mają taką samą długość.
C) Każdy kąt wewnętrzny dziesięciokąta ma miarę 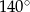 .
.
D) Obwód dziesięciokąta jest mniejszy od obwodu pięciokąta 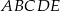 .
.
Długość jednego boku kwadratu 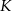 skrócono o 20%, a długość drugiego boku skrócono o 40%. W wyniku tych operacji otrzymano prostokąt
skrócono o 20%, a długość drugiego boku skrócono o 40%. W wyniku tych operacji otrzymano prostokąt 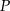 .
.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Stosunek długości przekątnej kwadratu 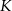 do długości przekątnej prostokąta
do długości przekątnej prostokąta 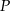 jest równy
jest równy
A) 0,48 B) 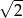 C) 1 D) 2
C) 1 D) 2
Krawędź podstawy ostrosłupa prawidłowego trójkątnego ma długość 4 cm, a wysokość jego ściany bocznej ma długość 5 cm.
Dokończ zdanie. Wybierz odpowiedź spośród podanych.
Pole powierzchni bocznej tego ostrosłupa jest równe
A) 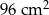 B)
B) 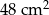 C)
C) 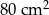 D)
D) 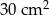
Trzydzieści piłeczek, ponumerowanych kolejnymi liczbami naturalnymi od 1 do 30, wrzucono do pudełka. Kacper, nie patrząc na piłeczki, wyjmuje je z pudełka. Ile najmniej piłeczek musi wyjąć Kacper, aby mieć pewność, że przynajmniej jedna wyjęta piłeczka jest oznaczona liczbą podzielną przez 4? Odpowiedź uzasadnij.
Przez punkty 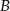 i
i 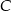 okręgu poprowadzono styczne, które przecięły się w punkcie
okręgu poprowadzono styczne, które przecięły się w punkcie 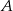 .
.
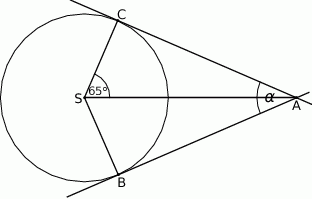
Oblicz miarę kąta 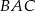 jeżeli
jeżeli 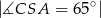 .
.
Na mecz siatkówki wybrała się grupa uczniów z opiekunami, razem 30 osób. Cena biletu normalnego dla opiekuna wynosi 40 zł, a bilet ulgowy dla uczniów jest o 20% tańszy. Łącznie za bilety zapłacono 1016 zł. Oblicz, ilu uczniów i opiekunów udało się na mecz. Zapisz obliczenia.
Pojemnik z kremem ma kształt walca o promieniu podstawy 5 cm i wysokości 5,12 cm. Po jego otwarciu okazało się, że krem wypełnia tylko wyżłobioną w pojemniku półkulę o promieniu 4 cm. Ile razy objętość tej półkuli jest mniejsza od objętości walca? Zapisz obliczenia.